目錄

🟨最大正方形

本題取自 Leetcode 221. Maximal Square

題目

Given an m x n binary matrix filled with 0’s and 1’s, find the largest square containing only 1’s and return its area.

Example 1:

Input: matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
Output: 4

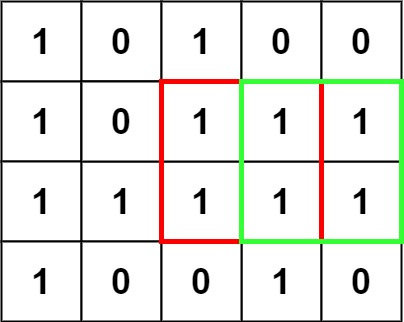
Example 2:

Input: matrix = [["0","1"],["1","0"]]
Output: 1

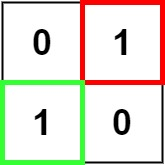
Example 3:

Input: matrix = [["0"]]
Output: 0
 

Constraints:

m == matrix.length
n == matrix[i].length
1 <= m, n <= 300
matrix[i][j] is '0' or '1'.

分析

題目要找出矩陣中，內部只包含'1'的最大的正方形面積。

分治法

考慮矩陣的第(i.j)格。以這格為右下角的最大正方形，其邊長為多少？

例如下圖綠底這格，其答案為2

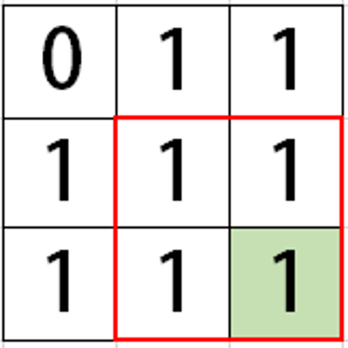
遍歷整個矩陣，並求每一格答案之最大值，即可得最大的正方形面積。

設計狀態、找出轉移式與最小問題

狀態：定義 maxSq(i,j)：

以矩陣的第(i.j)格為最右下角的最大正方形，其邊長。

轉移式

若matrix[i][j]=='0'，則這格不在任何正方形內， maxSq(i,j) = 0

若matrix[i][j]=='1'，則要進一步分析：

假設有一個邊長為k的正方形。若我們切掉右下角一格，則剩下的圖形能夠切出多大的正方形呢？

很顯然是k-1：

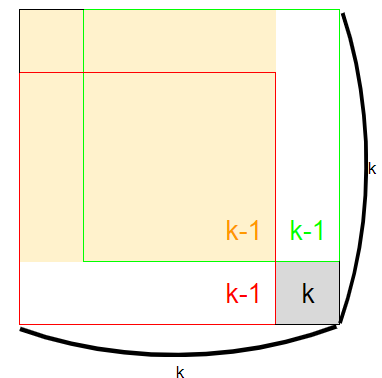
如果某格的答案為k(代表至少有一邊長為k的正方形)，則這格左上角、上方、左方一格的答案都應該至少為k-1

反過來想，若我們知道某一格左上角、上方、左方一格的答案，則右下角這一格的答案應該要怎麼求出來呢？

例如，考慮這個局部，數字是已求出的子問題答案(maxSq)：

根據我們對子問題的定義，可以知道周圍的圖形應該長這個樣子：

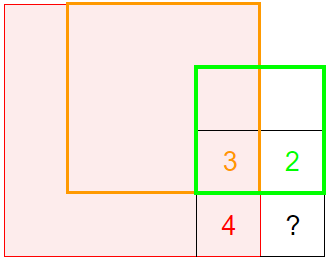
那麼問號這格的答案，很顯然應該是3

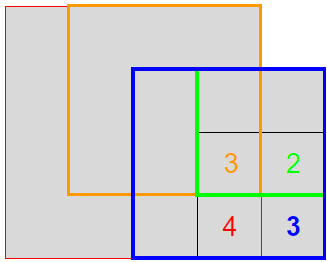
觀察之後，可以發現這個答案受限於上面這格的2，也就是說，子問題的答案受到左上角、上方、左方一格的答案之中的最小值的限制

某格的答案應為：左上角、上方、左方一格的答案之中的最小值 + 1

分析至此，我們終於可以得到完整的轉移式：

if matrix[i][j]=='0':
    maxSq(i,j) = 0
else: # (matrix[i][j]==1)
    maxSq(i,j) = 1 + min(
        maxSq(i-1, j-1) , maxSq(i-1, j) , maxSq(i, j-1)
    )

邊界條件：

當計算最上一列或者最左一行的子問題答案時(i==0 or j==0)，最大只會有邊長為1的正方形，因此maxSq(i,j) = matrix[i][j]

題目所求(母問題答案)：

題目所求為所有maxSq(i,j)中答案最大值的平方(求面積)

實作

Top-Down DP

class Solution:
    def maximalSquare(self, matrix: List[List[str]]) -> int:
        @cache
        def maxSq(i,j): # 以(i,j)為右下角的最大正方形邊長
            #  無正方形
            if matrix[i][j]=='0': return 0
            #  有正方形 (matrix[i][j]=='1')
            ## 最上一列 or 最左一行
            if i==0 or j==0: return 1
            ## 一般式
            return 1 + min(maxSq(i-1,j-1), maxSq(i-1,j), maxSq(i,j-1))
        # 回答：所有子問題之中答案最大者的平方
        return max(maxSq(i,j) for i in range(len(matrix)) for j in range(len(matrix[0]))) ** 2

Bottom-Up DP

class Solution:
    def maximalSquare(self, matrix: List[List[str]]) -> int:
        m,n = len(matrix), len(matrix[0])
        # 記錄子問題答案用的矩陣
        dp = [[0 for j in range(n)] for i in range(m)]
        maxAns = 0
        # 由上到下、由左到右計算每一格的子問題答案maxSq(i,j)並記錄於dp[i][j]
        for i in range(m):
            for j in range(n):
                #  無正方形
                if matrix[i][j]=='0': continue
                #  有正方形
                ## 最上一列or最左一行 
                if i==0 or j==0: 
                    dp[i][j] = 1
                ## 一般轉移式
                else:
                    dp[i][j] = 1 + min(dp[i-1][j-1], dp[i-1][j], dp[i][j-1])
                # 更新答案的最大值
                if dp[i][j]>maxAns:
                    maxAns = dp[i][j]
        # 回答：所有子問題之中答案最大者的平方
        return maxAns **2

因為狀態轉移只跟前一行、前一列的答案有關，本題也可以使用Rolling Bottom-Up DP

class Solution:
    def maximalSquare(self, matrix: List[List[str]]) -> int:
        m,n = len(matrix), len(matrix[0])
        # 記錄子問題答案用的矩陣
        dp = [0]*n
        maxAns = 0
        # 由上到下、由左到右計算每一格的子問題答案maxSq(i,j)並記錄於dp2[j]
        for i in range(m):
            dp2=[]
            for j in range(n):
                #  無正方形
                if matrix[i][j]=='0': 
                    ans = 0
                #  有正方形
                ## 最上一列or最左一行 
                elif i==0 or j==0: 
                    ans = 1
                ## 一般轉移式
                else:
                    ans = 1 + min(dp[j-1], dp[j], dp2[j-1])
                # 更新答案的最大值
                if ans > maxAns:
                    maxAns = ans
                dp2.append(ans)
            # Rolling
            dp = dp2
        # 回答：所有子問題之中答案最大者的平方
        return maxAns **2

複雜度分析

時間複雜度

時間複雜度 = 狀態轉移數 x 計算複雜度

本題的狀態數 = O(n^2)，計算複雜度 = O(1)

因此時間複雜度 = O(n^2)

空間複雜度

因為需要記住每題子問題的答案，空間複雜度 = 狀態數 = O(n^2)

如果使用Rolling的bottom-up，則空間複雜度 = O(n)

結語

和前兩天的矩陣問題不同，並非路徑相關的問題，而是和圖形判斷有關。

在這三天實作的過程我們可發現，矩陣題型有一些相似處：

• 狀態轉移和左方一格、上方一格有關(今天的題目還多了左上一格)
• 處理邊界條件時，需要考慮index超出邊界的情況
• Bottom-Up迭代的順序可以照著原矩陣的順序(例如筆者的範例解答，均從上到下並從左到右迭代)
• 可使用Rolling的技巧來幫Bottom-Up降低一個維度的空間複雜度

日後我們開始解Hard題時就會發現，許多進階的DP題都是結合基本題型和其他的演算法或者資料型態。

若能熟悉基本題型的共同點，並且掌握實作時需要注意的地方，在解進階題時會非常有幫助。

以上為Day08的內容！感謝你的閱讀，如果有不同的想法或心得，歡迎留言一同討論！

本文也同步登載在我的個人部落格，記錄我的學習筆記與生活點滴，歡迎來逛逛。

明天會開始看字串類型的問題。