🟨三角形

題目

Given a triangle array, return the minimum path sum from top to bottom.

For each step, you may move to an adjacent number of the row below. More formally, if you are on index i on the current row, you may move to either index i or index i + 1 on the next row.

Example 1:

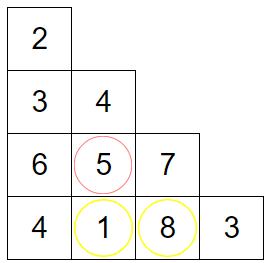
Input: triangle = [[2],[3,4],[6,5,7],[4,1,8,3]]
Output: 11
Explanation: The triangle looks like:
   2
  3 4
 6 5 7
4 1 8 3
The minimum path sum from top to bottom is 2 + 3 + 5 + 1 = 11 (underlined above).


Example 2:

Input: triangle = [[-10]]
Output: -10


Constraints:

1 <= triangle.length <= 200
triangle[0].length == 1
triangle[i].length == triangle[i - 1].length + 1
-10^4 <= triangle[i][j] <= 10^4

Follow up: Could you do this using only O(n) extra space, where n is the total number of rows in the triangle?

分析

和昨天的第二題(Leetcode 64. Minimum Path Sum)類似，本題求一個三角形矩陣從頂部往下走到底部的路徑中，最小的路徑和。

每一行的第j格，可以走到下一行的第j或者j+1格。

分治法

和昨天的第二題類似，我們可以定義子問題為：

從底部往上走到某(i,j)格(第i行第j格)，最小的路徑和為何？

根據規則，這一格可以經過下面一格((i+1,j))或者右下一格((i+1, j+1))，所以最小路徑和為：

下面這兩格的子問題答案中較小值 + 這一格本身的值

例如Example1測資紅圈這格，子問題答案 = 5 + min(1, 8) = 6

alt text

雖然題目描述的路徑是從頂部往下走，但因為計算路徑總和無關順序，所以我們規劃子問題時，反倒像是由底部往上走。

之所以這樣設計，是因為如果由下往上走，只會有一個終點，直接求這個終點的答案即可；但如果由上往下走，則有n個終點，需要額外再求一次這些終點答案中的最小值。

設計狀態、找出轉移式與最小問題

狀態：定義minPath(i,j)：

從底部往上走到某(i,j)格(第i行第j格)，最小的路徑和

轉移式：

minPath(i,j) = triangle[i][j] + min(minPath(i+1,j), minPath(i+1,j+1))

最小子問題(邊界條件)：

對於最下一列，minPath(i,j) = triangle[i][j]

母問題(題目所求)為minPath(0,0)

實作

Top-Down DP

需要@cache或者手動快取子問題的答案

class Solution:
    def minimumTotal(self, triangle: List[List[int]]) -> int:
        @cache
        def minPath(i,j):
            # 最下一列
            if i==len(triangle)-1: return triangle[-1][j]
            # 轉移式
            return triangle[i][j] + min(
                minPath(i+1,j), minPath(i+1,j+1)
            )
        return minPath(0,0)

Bottom-Up DP

class Solution:
    def minimumTotal(self, triangle: List[List[int]]) -> int:
        # 最後一列的答案
        dp = triangle[-1]
        # 由下往上計算每一列(從底部出發)的最小路徑和
        for i in reversed(range(len(triangle)-1)):
            # 記錄新的一列答案的空陣列
            dp2 = []
            # 由左往右逐格計算
            for j in range(i+1):
                # 狀態轉移式
                dp2.append(triangle[i][j] + min(dp[j], dp[j+1]))
            dp = dp2 # 捨棄掉用不到的前一列答案(rolling DP)
        # 回答母問題答案
        return dp[0]

由於測資的形狀特殊(三角形)，有一些和矩陣不同的細節需要注意：

因為我們由下往上計算，所以i要反過來從n-2迭代到0
三角形的每一列都不一樣長，第i列的格數為i+1而不是n

此外，因為題目在Follow up追加空間複雜度=O(n)的要求，我們使用滾動(Rolling) DP的技巧(類似於前幾天使用過的in-place DP)，捨棄掉已經不需要的列的答案，只記錄(目前計算到的)最新一列的答案。

複雜度分析

時間複雜度

時間複雜度 = 狀態轉移數 x 計算複雜度

本題的狀態數 = O(n^2)，計算複雜度 = O(1)

因此時間複雜度 = O(n^2)

空間複雜度

因為需要記住每題子問題的答案，空間複雜度 = 狀態數 = O(n^2)

如果使用Rolling的bottom-up，則空間複雜度 = O(n)

Top-Down要實現O(n)的空間複雜度比較麻煩，除了手動快取，還要修改遞迴函式用特定的遞迴順序來求解。有空間優化的需求時，通常會選擇能夠簡單控制計算順序的bottom-up。

🟨最小落下路徑總和

本題取自 Leetcode 931. Minimum Falling Path Sum

題目

Given an n x n array of integers matrix, return the minimum sum of any falling path through matrix.

A falling path starts at any element in the first row and chooses the element in the next row that is either directly below or diagonally left/right. Specifically, the next element from position (row, col) will be (row + 1, col - 1), (row + 1, col), or (row + 1, col + 1).

Example 1:

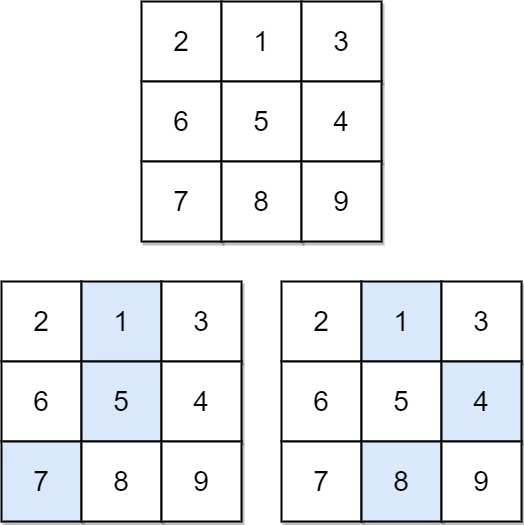
Input: matrix = [[2,1,3],[6,5,4],[7,8,9]]
Output: 13
Explanation: There are two falling paths with a minimum sum as shown.

alt text

Example 2:

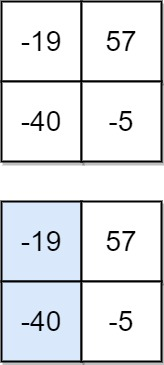
Input: matrix = [[-19,57],[-40,-5]]
Output: -59
Explanation: The falling path with a minimum sum is shown.

alt text

Constraints:

n == matrix.length == matrix[i].length
1 <= n <= 100
-100 <= matrix[i][j] <= 100

分析

和上一題(Leetcode 120. Triangle)幾乎相同，但走法變成可以往正下、左下、右下一格，並且圖形變成矩形，換言之有n個起點、n個終點。只需要稍微修改一下轉移式即可。

因為這題不是三角形，所以和前一題不同，不需要特別改成由下往上算。

分治法

子問題可定義成：從頂部的任一格往下走至某(i,j)格的最小路徑和。

設計狀態、找出轉移式與最小問題

定義狀態：minSum(i,j)表示從頂部的任一格出發，往下走至某(i,j)格的最小路徑和。

轉移式：每一格(i,j)是從上面(i-1,j)、左上(i-1,j-1)、右上(i-1,j+1)走來。因此：

minSum(i,j) = matrix[i][j] + min(minSum(i-1,j-1), minSum(i-1,j),minSum(i-1,j+1))

最小問題：最上一列minSum(0,j) = matrix[0][j]

題目所求：最下一列的所有子問題答案中的最小值

實作

Top-Down DP

class Solution:
    def minFallingPathSum(self, matrix: List[List[int]]) -> int:
        n = len(matrix) # 測資的長寬
        @cache
        def minSum(i,j):
            # 超出邊界的自動化處理
            if j<0 or j>=n: return float('inf')
            # 最上一列
            if i==0: return matrix[0][j]
            # 轉移式
            return matrix[i][j] + min(
                minSum(i-1,j-1), minSum(i-1,j), minSum(i-1,j+1)
            )
        # 最下一列子問題答案當中的最小值
        return min(minSum(n-1, j) for j in range(n))

由於題目的規則可以往左下、右下移動，如果要針對最左一行和最右一行去寫特別的轉移式也不是不行，但就是會覺得很麻煩。此時可以採用一個前面的題目中也出現過的技巧，就是當j<0 or j>=n時直接返回一個比所有測資都大的數float('inf')，讓(前一層)遞迴函式中的min自動排除掉這條路線。

在邊界條件複雜的題型中，並不針對每一個不同的邊界寫不同的轉移式，而是寫一個共通的轉移式，再對超出邊界的對象加以排除，這種寫法可以提升程式碼的邏輯可讀性。

Bottom-Up DP

class Solution:
    def minFallingPathSum(self, matrix: List[List[int]]) -> int:
        n = len(matrix) # 測資的長寬
        # 第一列答案
        dp = matrix[0]
        # 由上而下計算每一列子問題答案
        for i in range(1,n):
            # 紀錄下一列子問題答案的空陣列
            dp2 = []
            # 最左一格
            dp2.append(matrix[i][0]+min(dp[0], dp[1]))
            # 中間的每一格
            for j in range(1,n-1):
                dp2.append(matrix[i][j]+min(dp[j-1], dp[j], dp[j+1]))
            # 最右一格
            dp2.append(matrix[i][n-1]+min(dp[n-2], dp[n-1]))
            
            dp = dp2 # Rolling DP: 捨棄掉用不到的上一列答案
        # 最下一列子問題答案中的最小值
        return min(dp)

和前一題相同，本例使用Rolling DP來優化儲存空間。

上面的這種寫法，針對左右邊界寫了各自專用的轉移式，導致迴圈裡出現了三種不同的轉移式。如果想要仿照前一段(Top-Down DP)裡呈現的作法，只寫一個轉移式來提升邏輯可讀性，可以參考下面的作法：

class Solution:
    def minFallingPathSum(self, matrix: List[List[int]]) -> int:
        n = len(matrix) # 測資的長寬
        # 第一列答案
        dp = [float('inf')] + matrix[0] + [float('inf')]
        # 由上而下計算每一列子問題答案
        for i in range(1,n):
            # 紀錄下一列子問題答案的空陣列
            dp2 = [float('inf')]
            # 轉移式
            for j in range(n):
                dp2.append(matrix[i][j]+min(dp[j], dp[j+1], dp[j+2]))
            # 最右一格
            dp2.append(float('inf'))
            
            dp = dp2 # Rolling DP: 捨棄掉用不到的上一列答案
        # 最下一列子問題答案中的最小值
        return min(dp)

在記錄答案的陣列的最左、最右各「填充」一個大數float('inf')，這樣就算是在左邊界、右邊界的格子，計算時也可以套用相同的轉移式，來讓min自動排除掉超出邊界的情況。

但是要注意，由於左邊填充了一個數，所以dp陣列的index會往右平移一格，因此轉移式中取用dp答案的index也要全部跟著+1，換言之，不再是dp[j-1]~dp[j+1]，而是dp[j]~dp[j+2]

這種寫法還有個額外的好處是，可以搭配生成式寫得很pythonic：

class Solution:
    def minFallingPathSum(self, matrix: List[List[int]]) -> int:
        n = len(matrix) # 測資的長寬
        # 第一列答案
        dp = [float('inf')] + matrix[0] + [float('inf')]
        # 由上而下計算每一列子問題答案
        for i in range(1,n):
            # 轉移式
            dp = [float('inf')] + [matrix[i][j]+min(dp[j], dp[j+1], dp[j+2]) for j in range(n)] + [float('inf')]
        # 最下一列子問題答案中的最小值
        return min(dp)

複雜度分析

時間複雜度

時間複雜度 = 狀態轉移數 x 計算複雜度

本題的狀態數 = O(n^2)，計算複雜度 = O(1)

因此時間複雜度 = O(n^2)

空間複雜度

因為需要記住每題子問題的答案，空間複雜度 = 狀態數 = O(n^2)

如果使用Rolling的bottom-up，則空間複雜度 = O(n)

結語

我們今天繼續看了兩題矩陣路徑和的題目，希望能讓各位讀者更加熟悉矩陣的題型。

今天我們也再次演示了Rolling Bottom-Up DP，這個技巧可以幫助減少空間複雜度(通常能降低一個維度)，對於用空間換取時間的動態規劃演算法來說，顯然CP值更高了，是一個適合使用時就建議盡量使用的技巧。(但時間複雜度並沒有改變！)

並且，在第二題的最後，我們看到一種「填充邊界」的資料處理技巧。這個方法的好處可以改善Bottom-Up原本需要對邊界去寫不同轉移式/條件判斷式的小痛點，讓轉移式的邏輯更有可讀性，搭配Python的列表生成式，能夠讓Bottom-Up的語法寫起來和Top-Down一樣精簡，並使得轉移式的邏輯一目了然。

以上為Day07的內容！感謝你的閱讀，如果有不同的想法或心得，歡迎留言一同討論！

本文也同步登載在我的個人部落格，記錄我的學習筆記與生活點滴，歡迎來逛逛。

明天會看一些不是求路徑和的矩陣題型。

[2024鐵人賽系列文] Python刷題小白的30日動態規劃之旅－Day 07 矩陣題型(中)

目錄

🟨三角形

題目

分析

分治法

設計狀態、找出轉移式與最小問題

實作

Top-Down DP

Bottom-Up DP

複雜度分析

時間複雜度

空間複雜度

🟨最小落下路徑總和

題目

分析

分治法

設計狀態、找出轉移式與最小問題

實作

Top-Down DP

Bottom-Up DP

複雜度分析

時間複雜度

空間複雜度

結語

夏