目錄
圓周率日
除了眾所周知的西洋情人節,在每年的3月14日數學家們也會歡慶這個日子。
不只是數字恰與圓周率相同,這一天還與兩位為人類帶來卓越貢獻的物理學家有關,今天是愛因斯坦的生日,也是霍金去世的日子,這些巧合為這個日子增添了傳奇的色彩。
小學時我們便學過「圓周率」,亦即圓形的「周長」與「直徑」的比值,並了解到它屬於「無理數」,也就是無法以「兩個整數相除」(分數)來表示的實數。
作為一個純粹的「數學常數」,π=3.1415926...的這個「事實」似乎不證自明,但你可曾想過:π竟然與物理中「地表重力加速度」g有著驚人的「前世姻緣」!
g
g,地表重力加速度,也等於地表重力場的大小。在高一物理中我們學到g和星球的質量與半徑有關:
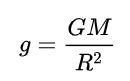
其中,G是萬有引力常數(6.6743×10^−11 m^3 / kg s^2),M是星球質量,R是星球半徑。將以上數值代入,就可以得到在星球表面的重力加速度。
若M代入地球質量(5.972x10^24 kg),R代入地球半徑(6.371x10^6 m),就可以得到地表的重力加速度g = 9.8199
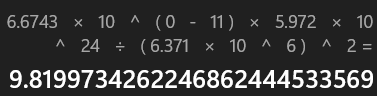
(實際上科學界採用的數值是9.806,因為在地球自轉的非慣性坐標系中,以慣性坐標系思考問題時要加入假力,因此還要扣除地球自轉所造成的的離心力)
因為隨著緯度、高度、地底岩層密度等等因素,世界各地重力都會有所不同,在高中解題時我們都是以平均值來計算。有興趣的同學也可以探究一下這三個因素對重力加速度的影響分別是什麼。
話題回到π:按一下計算機就會發現,把g開根號之後的數值「差不多」就是π。

這…只是巧合吧?而且也只是差不多相等呀。
對於這個「巧合」,你的直覺判斷是否也是這樣呢?
畢竟這個g只是「地球表面」的重力加速度,比如說在月球表面,g值就只有地球表面的1/6,若到太陽表面,g值有地球的30倍,若是在黑洞的「史瓦西半徑」上,重力更是大到連光都無法逃離。
這樣一個「因地制宜」的g,和數學裡「不證自明」的常數π,怎麼會有因果關係呢?
但實際上,這並不只是巧合。或者更嚴謹地說,這是由一個「人為定義」最終造成的結果。
多探究可以提升同學的數理素養,放個防雷頁,程度好的同學可以先不要往下看,和班上同學一同討論、探究看看背後的原因!

影響g值大小的「隱藏要素」
前面提到,g值受到星球半徑與質量的影響。
但就算我們將地點限定於地球表面,也就是固定了前述的兩個因子,「地表重力加速度」的g仍然可能「不是9.8」!
箇中關鍵就在於:g是一個有「單位」的物理量。
高一物理的課程中,一定會討論到「物理量」和數學數值的差異:
物理量 包含 「數值」與「單位」(若是向量,還包含「方向」)
舉例來說,假如筆者定義一個新的長度單位,「長」(long),並且「1長=0.94公分」,那麼筆者的身高也能有180了!(只是,是180「long」而不是180「cm」)
改變單位本身所代表的大小時,所有用這個單位所描述的物理量(的數值)都會跟著變化。而且,這個改變並不僅止於我們測量物體所得到的量,連「物理常數」的數值也會跟著改變。
給看不懂的你:其實就只是「單位換算」啦。
回到我們的問題,pi和根號g之所以如此相近,背後的秘密在於:
吾人定義了「公尺」與「秒」的單位,才使得重力加速度
g = 9.8(m/s^2)
π是數學常數,其值永遠是3.14…,然而g是物理常數,其值取決於人類對於單位的定義。而9.8這個數值所代表的單位系統,是我們熟悉的MKS制,也就是公制單位,在高中課堂中,我們更學到這是一套包含七個基本單位的「SI單位制」系統。
公尺制的演變史
故事要從SI制中的基本單位「公尺」的定義聊起。
早在17世紀,伽利略研究鐘擺運動的規律性,並發現單擺的周期僅與其長度有關。西元1671年,法國科學家測量「秒擺」,即一秒擺動一次的單擺的長度,並建議使用這個長度的兩倍作為新的統一長度單位toise universelle。1675年,科學家布拉蒂尼提議用術語metro cattolico(直譯為通用測量)來表示這個單位。
在法國大革命之前,法國境內的度量衡尚未統一,1789年大革命成功之後,國民公會指示巴黎科學院訂下一個新的長度標準,除了有利於民生及學術發展,也作為掃除舊政權的改革象徵。巴黎科學院考量了「單擺擺長」的定義,但當時便已知,單擺的周期會受到所在地重力值的影響而有所不同,這和新單位「全國一致」的期望已不相符。
因此,巴黎科學院決定基於以下事實來提出新的單位公尺(mètre):地球的周長大約為2千萬toise。
1公尺定義為:本初經線(0度經線)北極點至赤道的長度的1千萬分之一
換言之,在最後採用的定義中,1公尺大約為0.513 toise,也就是「大約」為秒擺的擺長。
但地球的半徑亦非永恆不變,因此在對經線長度做了精確測量之後,科學家就鑄造了一根銥鉑合金的公尺原器,作為1公尺的標準。(也就是一把1公尺的尺啦。)
不過科學家又發現,用實體物品來定義單位終究不是長遠之計,比如原器遺失、或隨著時間磨損等等都會造成難以回溯的誤差。因此在1960年,改以電子在原子軌域間躍遷所放出的特定頻率光波的「波長」的整數倍來定義,隨後在1983年再更改為如今的光速定義。
這些後續的定義演變可以參考高一物理的課程內容(考試會考!),不過先讓我們回到π與g的愛恨情仇,把目光放在這段歷史的開頭,公尺與它的前身toise有這樣的關係:
1公尺 = 0.513 toise
又,根據toise原本的定義
1 toise = 秒擺擺長的兩倍
換言之,假如法國科學院當年採用了基於「單擺」的定義,那麼:
1公尺 = 秒擺的擺長 (在採用單擺定義的平行時空)。
單擺公式,擦身而過的π與g
在高二物理,我們會學到:當單擺的擺角很小時,其擺動周期與底下懸掛的重物質量無關,並且有下列關係:
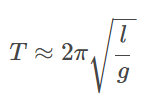
其中,T為單擺「來回」擺動(擺錘回到原點)的周期,l為單擺的擺長,而g為實驗當地的重力加速度。
(相關推導省略,可參考高二選修物理的課本內容)
我們把基於秒擺的公尺定義帶進來看看:
「秒擺」指的是單擺擺動1次(單趟)花費1秒的單擺,因此,來回一趟的週期為2秒。其長度(大約)為1公尺。
因此,上面的公式中,T代入2,l代入1。發現了嗎?
經過移項,我們可以得到:
根號 g ≈ π
物理常數g與數學常數π,因為人類對於「公尺」的定義,建立起了如此美妙的數學關係。
為了避免各位同學誤解,強調一下:
- 由於當年最終並不是採用單擺的定義,SI單位制的1公尺只是「近似」秒擺擺長,而非完全等於。(這個因素影響比較大)
- 單擺公式並非等號,而是近似符號,這是因為推導的過程中將單擺運動「近似」於簡諧運動。詳見高二物理課本內容。
由於這兩個因素,地表重力加速度的值9.806開根號3.13...,儘管如此相近,還是跟數學常數π失之毫釐。
結語
在白色情人節的今天,細思π與公尺制的發展歷史,數學常數的π與物理常數的g,兩人只差一步就能共渡未來,最終卻因人類的選擇而擦身而過,這又何嘗不是一齣浪漫的科學悲戀呢?