今天 (4/12) 的 Daily 是 Hard 題： Leetcode 42. Trapping Rain Water

目錄

題目分析

題目

Given n non-negative integers representing an elevation map where the width of each bar is 1, compute how much water it can trap after raining.

Example 1:

Input: height = [0,1,0,2,1,0,1,3,2,1,2,1]
Output: 6
Explanation: The above elevation map (black section) is represented by array [0,1,0,2,1,0,1,3,2,1,2,1]. In this case, 6 units of rain water (blue section) are being trapped.

Example 2:

Input: height = [4,2,0,3,2,5]
Output: 9

Constraints:

n == height.length
1 <= n <= 2 * 10^4
0 <= height[i] <= 10^5

分析

儲水問題，給定地形問能儲存的最大水量。

基本上Ex1的圖就清楚呈現在問什麼了。

思路一、暴力解(Brute Force)

解題策略

假設h[i] 給出第i格的池底高度。

根據常識，假設在第i格能夠儲水，代表：

在i的左邊、右邊，至少都要有一格，其池底高度高於i這格的池底高度。

水槽總要有壁才不會漏水對吧。

換言之，須滿足以下條件：

1. 存在至少一j，使 j<i，且 h[j]>h[i]

2. 存在至少一k，使 k>i，且 h[k]>h[i]

那這格可以儲多少的水量呢？

可以直接考慮這一格的水面位置top，發現：

在i右邊所有的格子中最高的一格，其高度為 highest_right

在i左邊所有的格子中最高的一格，其高度為 highest_left

則i這格的水面高度top，必定是 min(highest_left,highest_right)

池底高度就是h[i]

每格的寬度為1，因此這格的水量就是(top-h[i]) x 1

如此分析，就先得到一個暴力解的思路：

逐格檢查這格能不能儲水，若可以，則檢查這格能儲多少水，最後再加總即為答案。

程式碼範例(Python3)

class Solution:
    def trap(self, height: List[int]) -> int:
        def hasBorders(i):
            if i==0 or i==len(height): return False
            return (
                any(height[j]>height[i] for j in range(0,i)) 
                and
                any(height[j]>height[i] for j in range(i+1, len(height)))
            )
        def top(i):
            return min(
                max(height[j] for j in range(0,i)), # highest_left 
                max(height[j] for j in range(i+1, len(height))) # highest_right
            )
        return sum((top(i)-height[i]) for i in range(len(height)) if hasBorders(i))

不過這個解法會吃TLE。

究其原因，在於我們在每一格計算top時，都需要重新計算最大左右邊界highest_left與highest_right。

複雜度分析

遍歷height計算每一格的水量，時間複雜度O(n)

每次計算top需要遍歷整個height，時間複雜度O(n)

因此總時間複雜度為O(n^2)

思路二、利用 Monotonic Stack 的動態規劃法

Monotonic Stack 單調堆疊(遞增/遞減堆疊)介紹

Monotonic指的是數字上的遞增/遞減。

Monotonic Stack，指在建立Stack的過程之中，保證這個Stack的元素維持(嚴格)遞增/遞減的性質。

舉例來說，我們有一個陣列nums=[1,0,4,5,9,3,6]與一個空的堆疊stack=[]

目標：將nums的元素依序入棧(push)，過程中保證stack內的元素保持嚴格遞增數列的性質

要怎麼做呢？

很簡單，只要在每一個元素入棧之前，持續檢查stack最後一個(最外面)的元素。

• 假如尾端元素>=新元素，就將尾端元素出棧(pop)

直到陣列為空，或者尾端元素<新元素為止，並將新元素入棧(push)。

如此一來，便保證在新元素依序入棧的過程中，stack恆為一個嚴格遞增數列。

以Python簡單實作看看：

nums=[1,0,4,5,9,3,6]
stack=[]

for n in nums:
    while stack and stack[-1] >= n:
        stack.pop()
    stack.append(n)
    print(stack)

透過print的結果我們可以觀察在依序入棧的過程，stack維持嚴格遞增的性質。

nums=[1,0,4,5,9,3,6]
stack=[]

for n in nums:
    while stack and stack[-1] >= n:
        stack.pop()
    stack.append(n)
    print(stack)

當然，根據使用目的不同，也可以維護一個嚴格遞減數列，亦可以不必嚴格(接受等於)，只需要修改檢查時(while迴圈)的比對條件即可。

熟悉了 Monotonic Stack 之後，就可以在動態規劃演算法中應用這個資料結構。

One-Pass Dynamical Progamming 思路

遍歷height，同時維護一個 monotonic stack 來紀錄index，讓height[index]始終維持一個嚴格遞減數列。

之所以紀錄index而不直接紀錄height的值，在於後續計算水量時還會用到index。這在應用 Monotonic Stack 的動態規劃法中也是滿常見的實作。

i=0時，

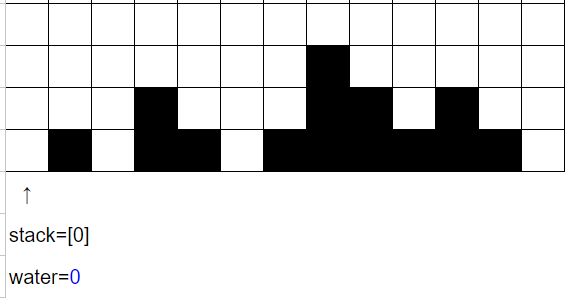
原本stack為空，代表左端沒有比自己低的「水槽」，因此儲水量並沒有增加。維護stack讓index=0入棧。

i=1時，

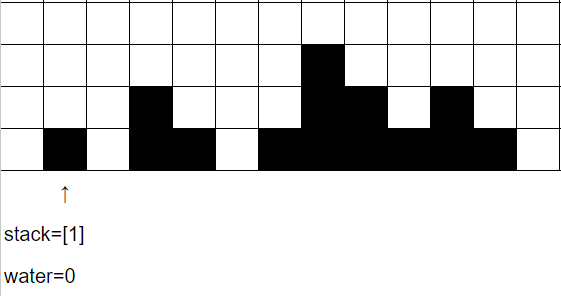
height[stack[0]] = 0代表左邊最高的牆壁，因此儲水量並沒有增加。

維護stack讓index=0出棧，1入棧

i=2時，

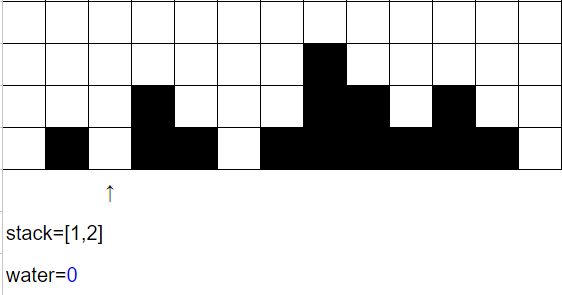
維護stack讓index=2入棧

i=3時，

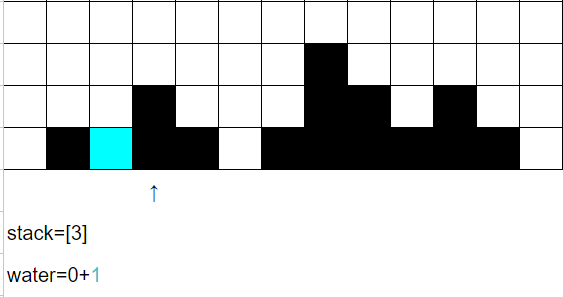
在此之前的stack=[1,2]，其最尾端所代表的高度 height[2] = 0比此時的h=2來得低，代表出現了一個「水槽」。

維護stack，讓index=2出棧，同時這個數字也代表水槽「最右端」的位置right

此時stack剩下[1]

水槽的寬度：

• 此時stack中最後一個index，stack[-1]=1，代表「最靠右」的牆壁在1的位置，也就是水槽最左端的牆壁left。

• 兩者相減即為水槽寬度 width = (right - left)

• (因為right是水槽 left是牆壁，所以不用-1)

水面的高度：

• stack[0]=1是左端牆壁的位置，因此height[1]=1是左端牆壁的高度
• 此時的i=3是右端牆壁，因此height[3]=2是右端牆壁的高度
• 兩者中較小的即為水面高度。即top=min(height[stack[0]], height[i])

池底的高度：

• 剛才出棧的right，其高度即為池底高度。即bot=height[right]

儲水的水深：

• depth = top-bot

增加的水量：

• water += width * depth

最後維護stack讓i=3入棧。

i=4時，

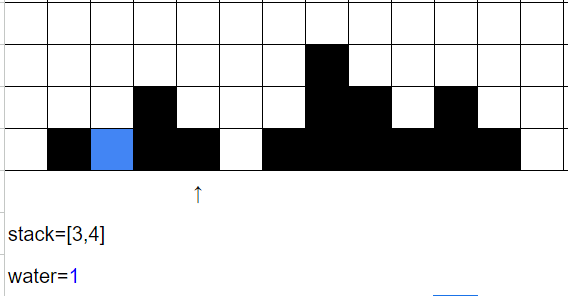
維護stack讓i=4入棧

i=5時，

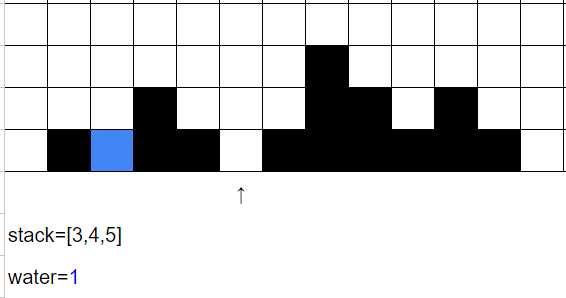
維護stack讓i=5入棧

i=6時，

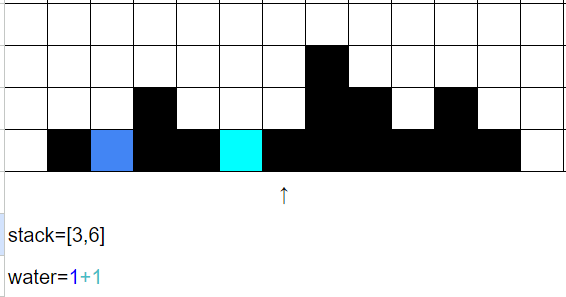
跟i=3類似，一邊維護stack一邊計算水量，最後再讓i=6入棧。

i=7時，

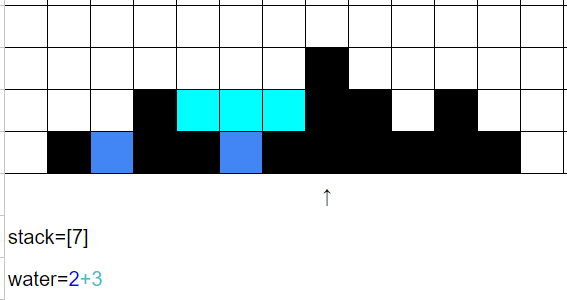
跟i=3類似，一邊維護stack一邊計算水量，最後再讓i=7入棧。

注意此時我們計算的跟i=6「實際上」是同一個水槽，但是「一部分的水量」(圖上深藍色的部分)已經在i=6時計算過，只計算「「新形成的儲水空間」(圖上淺藍色的部分)。

這就是為什麼本題需要用到monotonic stack：

我們要由深至淺、由右而左計算水量

stack出棧的順序是「由右而左」(由新往舊)

monotonic遞減的特性保證在這個「倒著」出棧的過程中，池底深度越來越高(遞增)

程式碼範例(Python3)

class Solution:
    def trap(self, height: List[int]) -> int:
        water = 0
        stack = []
        for i, h in enumerate(height):
            if stack:
                top = min(h,height[stack[0]])
            while stack and h >= height[stack[-1]]:
                right = stack.pop()
                if stack:
                    left = stack[-1]
                    bot = height[right]
                    water += (right - left) * (top - bot)
            stack.append(i)
        return water

複雜度分析

在過程中每個index只會入、出棧一次，因此時間複雜度為T=O(n)

stack最大的長度為height的長度，因此空間複雜度為S=O(n)

結語

真的很喜歡 Monotonic Stack 的思路，所以剛好這題在 daily 出現就忍不住寫了一篇 XD

感謝你的閱讀，如果有不同的想法或心得，歡迎留言一同討論！