今天 (2/24) 的 Daily 是 Hard 題： Leetcde 2092. Find All People With Secret

目錄

題目分析

題目

You are given an integer n indicating there are n people numbered from 0 to n - 1. You are also given a 0-indexed 2D integer array meetings where meetings[i] = [xi, yi, timei] indicates that person xi and person yi have a meeting at timei. A person may attend multiple meetings at the same time. Finally, you are given an integer firstPerson.

Person 0 has a secret and initially shares the secret with a person firstPerson at time 0. This secret is then shared every time a meeting takes place with a person that has the secret. More formally, for every meeting, if a person xi has the secret at timei, then they will share the secret with person yi, and vice versa.

The secrets are shared instantaneously. That is, a person may receive the secret and share it with people in other meetings within the same time frame.

Return a list of all the people that have the secret after all the meetings have taken place. You may return the answer in any order.

Example 1:

Input: n = 6, meetings = [[1,2,5],[2,3,8],[1,5,10]], firstPerson = 1
Output: [0,1,2,3,5]
Explanation:
At time 0, person 0 shares the secret with person 1.
At time 5, person 1 shares the secret with person 2.
At time 8, person 2 shares the secret with person 3.
At time 10, person 1 shares the secret with person 5.​​​​
Thus, people 0, 1, 2, 3, and 5 know the secret after all the meetings.

Example 2:

Input: n = 4, meetings = [[3,1,3],[1,2,2],[0,3,3]], firstPerson = 3
Output: [0,1,3]
Explanation:
At time 0, person 0 shares the secret with person 3.
At time 2, neither person 1 nor person 2 know the secret.
At time 3, person 3 shares the secret with person 0 and person 1.
Thus, people 0, 1, and 3 know the secret after all the meetings.

Example 3:

Input: n = 5, meetings = [[3,4,2],[1,2,1],[2,3,1]], firstPerson = 1
Output: [0,1,2,3,4]
Explanation:
At time 0, person 0 shares the secret with person 1.
At time 1, person 1 shares the secret with person 2, and person 2 shares the secret with person 3.
Note that person 2 can share the secret at the same time as receiving it.
At time 2, person 3 shares the secret with person 4.
Thus, people 0, 1, 2, 3, and 4 know the secret after all the meetings.

Constraints:

2 <= n <= 10^5
1 <= meetings.length <= 10^5
meetings[i].length == 3
0 <= xi, yi <= n - 1
xi != yi
1 <= timei <= 10^5
1 <= firstPerson <= n - 1

分析

秘密一旦告訴一個人就不是秘密了XD

問題相當單純：

每個meetings[i]=[x,y,t]代表x與y在t時間產生交流

t=0時，第0與第firstPerson知道了秘密

在任何時間t，若某個人知道秘密，就會立刻和「所有正在與自己交流的人」共享秘密。

求最後知道秘密的所有人。

1. 無向無權重圖

   首先，對圖論稍微有概念的話，應該很容易發覺這是一個圖論題。

   如果把每一個人當作節點(Node)，那麼每個meeting就是將人與人串聯起來的邊(Edge)。

   只要和「知道秘密的人」透過 邊 與 其他節點(其他人) 相連在一起，就會變成也知道秘密。

   可以說這是一種沿著圖傳播的「秘密廣播」(broadcasting)

   對於任意的邊(meeting)上面的兩個節點(人)，假設其為x,y，則：

   x知道秘密會告訴y，y知道秘密也會告訴x。

   圖上的邊不具有方向性，或者說具有雙向性，換言之，可以用一張「無向圖」來模擬本題所有的「人際關係」(meetings)

   以Ex1的測資為例：

    n = 6, meetings = [ [1,2,5],[2,3,8],[1,5,10] ], firstPerson = 1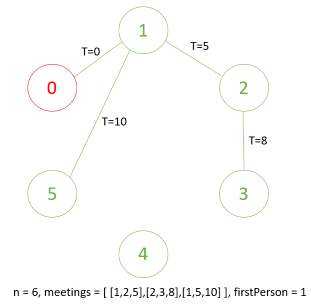
   

   

2. 時間維度

   本題之所以為 Hard，在於題目加上了時間尺度：隨著時間推進，知道秘密的人越多，而在任何時間，只要和任何「知道秘密的人」進行會議，自己也會成為知道秘密的人。

   在t=0時，0會告訴1秘密

   

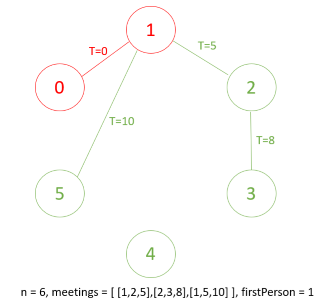
   在t=5時，1告訴2秘密

   

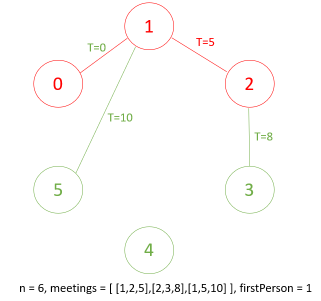
   在t=8時，2告訴3秘密

   

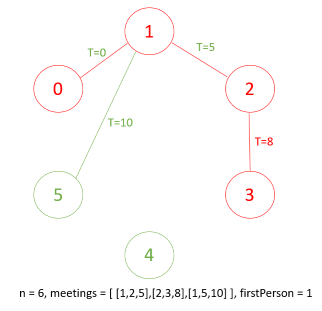
   在t=10時，1告訴5秘密

   

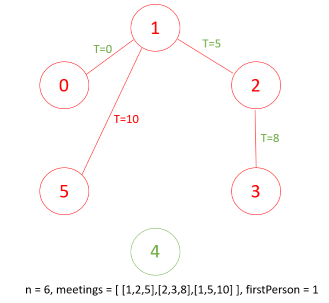
   因此最終知道秘密的人有[0,1,2,3,5]

3. 樹

   從上述舉例可以發現，我們可以把「知道秘密的人」用紅色線連起來，組成一顆「樹」。隨著時間推進，進行一次又一次的meeting(連線)，只要有某個節點連接上這棵紅色的樹，就會立刻成為這棵樹的一部分，而在最終這棵樹的成員也就是答案。

透過以上分析，求解本題需要做三件事情：

1. 要能從每個節點「查詢」其不同時間的「相鄰節點」

   換言之，跟所有圖論演算法的問題一樣，要「建立」圖。

   可以使用Hashmap，將每個節點作為key，並將其value設為一個array，用來存放所有與之相鄰的節點。

2. 按照時間順序「連線」

   換言之，需要對時間做排序

3. 隨著時間，要記錄「知道秘密的人」的這棵樹，並且在任意的時間，要能夠查詢某個節點和樹是否相連。

   在圖上查詢兩個節點(或兩棵樹)是否相連

解題思路

方案一 照時間順序的 Broad First Search

因為解法很長，本文先將程式碼po出，再逐步進行解釋。

範例程式碼

# Greedy: Union Find
class Solution:
    def findAllPeople(self, n: int, meetings: List[List[int]], firstPerson: int) -> List[int]:
        def tell(edges: List[List[int]]) -> None:
            t = defaultdict(set)
            tellers = set()
            for x,y in edges:
                t[x].add(y)
                t[y].add(x)
                if knows[x]: tellers.add(x)
                if knows[y]: tellers.add(y)
            while tellers:
                listeners = set()
                for x in tellers:
                    for y in t[x]:
                        if knows[y]: continue
                        knows[y] = True
                        listeners.add(y)
                tellers = listeners

        meetings.sort(key = lambda x:x[2])

        knows = [False]*n
        knows[0], knows[firstPerson] = True, True

        i, m = 0, len(meetings)  
        while i<m:
            partners = []
            time = meetings[i][2]
            while i<m and time == meetings[i][2]:
                x,y,_ = meetings[i]
                if not knows[x] or not knows[y]:
                    partners.append((x,y))
                i += 1
            tell(partners)
        
        return [i for i in range(n) if knows[i]]

演算法說明

1. 對meetings按照時間進行排序

   meetings.sort(key = lambda x:x[2])

2. 以一個陣列knows記錄「目前為止，這個人是否知道秘密」

3. 從第 i = 0場 meeting 開始遍歷meetings，並且同時考慮所有「在相同時間發生的meeting」。

   之所以要同時考慮，是因為若某人在某時間聽到這個秘密，且同時這個人還有其他的會議，那他也會在同時間將這個祕密傳播出去。所以，同一時間進行的所有會議都要一起考慮。

   while i<m and time == meetings[i][2]:

4. 在時間time，如果某場會議的雙方都已經知道秘密，那就不需要管這場會議。如果會議中的任一方，或者雙方都還不知道秘密，那麼就把這場會議加入「一起考慮清單」partners。

   if not knows[x] or not knows[y]:
       partners.append((x,y))
   

5. 同時考慮所有：在時間time進行的會議partners，讓這些會議之中，所有知道秘密的人都把秘密說出來tell(partners)

   BFS

   def tell(edges: List[List[int]]) -> None:
   

   1. 建立圖 t = defaultdict(set)

      for x,y in edges:
          t[x].add(y)
          t[y].add(x)
          if knows[x]: tellers.add(x)
          if knows[y]: tellers.add(y)
      

   2. 同時記錄知道秘密的人 tellers

   3. 讓tellers把祕密告訴所有他們的鄰居(一起參加會議的人)

      while tellers:
          listeners = set()
          for x in tellers:
              for y in t[x]:
                  if knows[y]: continue # 原本就知道秘密，跳過
                  knows[y] = True       # 現在才知道秘密
                  listeners.add(y)
      

   4. 同時，把原本不知道秘密，但現在知道秘密的人，紀錄為listener

   5. listener也會立刻再把秘密告訴他們的鄰居，因此，

      while tellers:
      
          ...
      
      tellers = listeners
      

      重複步驟(3)~(5)直到沒有新的listeners

6. 重複步驟3~5直到所有meeting都結束

如果被三個 while 迴圈繞得暈頭轉向，建議搭配 [題目分析－分析]這段的圖解會比較容易理解。

複雜度分析

步驟1的排序時間複雜度為 T = O(m log m)，m為meetings的長度(邊的總數)

步驟2~6的三層while，其實只對整個meetings遍歷一次。因此，效能關鍵在於while tellers執行的次數與時間。

在while tellers區段，每個node(人)x都有機會被加入一次tellers，因此後半段總時間複雜度最高為T = O(n x m)，其中m為meetings的長度(邊的總數)，n為總人數。

因此，總時間複雜度為T = O( m x(log m + n) )

方案二 照時間順序的 Union Find + Reset

方案一在每個獨立的時間中「判斷是否知道秘密」的流程，可以從BFS優化為Union Find

Union Find 介紹

Union Find又稱為Disjoint Set，顧名思義是要判斷兩棵樹是否相連(兩個集合是否有交集)。

要實作 Union Find，可以用 Tree 有唯一Root的概念，並賦予以下操作：

1. 以root來代表一顆獨立的樹

2. find(x)：每個節點都可往上尋找自己的parent，最終找到自己歸屬的root

3. connected(x,y): 判斷x,y所在的是否為同一顆樹。

4. unite(x,y)：如要將兩棵不同root的樹AB上的點x,y連通，可以將A樹的root設定為B樹的parent。如此一來，所有原本B樹上的節點，其find都會找到A樹的root。

5. rank：如果unite的時候採取隨機方式來連接，那麼將會遇到這種worst case：

   總是將較長的tree接到較短的tree的root上，從而導致tree樹無意義的增加。

   由於find對任意節點遍歷的時間複雜度為O(所有樹以成員數量做加權平均的樹高)，會希望最小化平均樹高以優化效能。

   因此定義rank：rank[i] = 以i為root的樹的高度。

   並且每當進行unite時，總是將rank小的樹連接至rank大的樹的root上，如此一來即可維持大樹的樹高不變。唯有當兩顆樹rank相當時樹高才會增長為rank+1。

6. reset：將樹(集合)解散時，即將節點的parent重新設定為自己，並且將rank重置為0。

   本題在每個獨立時間結束之後，若某顆樹(某群彼此因為一同參與會議而相連的人)，若其中的所有人均不知秘密(尚未連接至i=0的樹)，則在下一個獨立時間開始前，他們仍不知秘密。因此需要把樹解散，以避免過去時間的連接(會議)造成未來時間的秘密透漏。

範例程式碼：

sort與兩層while迴圈基本上只為了找出相同時間舉行的會議

接著對於每個獨立的時間的所有會議進行Union Find

在下個時間開始之前解散所有未與節點0相連(未知秘密)的會議

class Solution:
    def findAllPeople(self, n: int, meetings: List[List[int]], firstPerson: int) -> List[int]:
        # 圖初始化
        graph = UnionFind(n)
        graph.unite(firstPerson, 0)

        # 會議依照時間排序
        meetings.sort(key=lambda x: x[2])

        # 找出在每個時間 進行的 所有會議
        i, m = 0, len(meetings)  
        while i<m:
            partners = []
            time = meetings[i][2]
            while i<m and time == meetings[i][2]:
                x,y,_ = meetings[i]
                partners.append((x,y))
                i += 1

            # Union Find
            for x, y in partners: 
                graph.unite(x, y)

            # 如果仍不知道秘密，就重設這個節點
            for x, y in partners:
                if not graph.connected(x, 0):
                    graph.reset(x)
                    graph.reset(y)
        
        # return 答案為所有與0相連的節點
        return [i for i in range(n) if graph.connected(i, 0)]

class UnionFind:
    def __init__(self, nodes: int):
        # 初始化圖(每個節點的parent為自己，rank為0)
        self.parent = [i for i in range(nodes)]
        self.rank = [0] * nodes

    def find(self, x: int) -> int:
        # 遞迴尋找節點x的root
        if self.parent[x] != x:
            self.parent[x] = self.find(self.parent[x])
        return self.parent[x]

    def unite(self, x: int, y: int) -> None:
        # 若x與y所在的樹不相連，則將其相連
        px = self.find(x)
        py = self.find(y)
        if px != py:
            # 將rank小的樹連接至rank大的樹根
            if self.rank[px] > self.rank[py]:
                self.parent[py] = px
            elif self.rank[px] < self.rank[py]:
                self.parent[px] = py
            else:
                self.parent[py] = px
                self.rank[px] += 1
    
    def connected(self, x: int, y: int) -> bool:
        # 判斷x與y所在的樹是否相連
        return self.find(x) == self.find(y)
    
    def reset(self, x: int) -> None:
        # 重設節點x
        self.parent[x] = x
        self.rank[x] = 0

複雜度分析

Sorting的時間複雜度為T = O(m log m)

初始化圖的時間複雜度為T = O(n)

後續的雙重while迴圈以及其中Union Find的部分，實際上只對每場meeting遍歷兩次(Unite 與 Reset各1次)(O(m))。對於每次Unite與Reset操作，經過平均後的時間複雜度可以近似常數時間O(1)。因此整個Union Find 區段的時間複雜度為O(m)

最後遍歷所有的i(O(n))檢查是否與0號節點Connected的複雜度，每次操作經過平均後可以近似為O(1)，因此這個區段的時間複雜度為O(n)

因此，總時間複雜度為T = O(m log m)

空間複雜度則僅需建立圖的S = O(n)

僅管本題的公式最佳解為方案二，但因為實作Union Find有較大的常數時間成本，讓其他方法並沒有比較差。筆者還想到一個貪心搭配binary search和Heap的做法。

方案三、Greedy (Broadcasting)

主要概念是這樣的：前面兩種做法都是先將會議用時間排序，再拿相同時間的所有會議去建立圖，執行圖論演算法(BFS或者Union Find)。

但其實，也可以先無視時間建立圖，再對時間做排序。

已知：

1. 假設某個節點A在時間t知道秘密，則在包含t與之後的所有時間，和A一起會議的所有人都會知道。
2. 假設有許多人可能在不同的時間告知節點A秘密，則只需要關心A「第一次知道秘密」的時間點。在這時間之前A所參與的會議都無須理會。

以Ex1的測資為例：

 n = 6, meetings = [[1,2,5],[2,3,8],[1,5,10]], firstPerson = 1


 將(時間0,告訴1)放入heap

 t=0 
 考慮節點1：「最早」在時間0知道秘密。因此在時間5告訴節點2。在時間10告訴節點5

 將(時間5,告訴2)與(時間10,告訴5)放入heap

 t=5
 考慮節點2：「最早」在時間5知道秘密，因此在時間8告訴節點3

 將(時間8,告訴3)放入heap

 t=8
 考慮節點3：「最早」在時間8知道秘密

 t=10
 考慮節點5：「最早」在時間10知道秘密

注意到這裡我們使用了min heap (priority queue)來維持「下一個會知道秘密的人」。

筆者認為，比起需要學過才會懂得圖論演算法，這裡貪心的思路是更接近人腦對這個問題直覺的。

其實是覺得要把Union Find碼出來很麻煩才先想到這種作法(X)

範例程式碼

Greedy: broadcasting

class Solution:
    def findAllPeople(self, n: int, meetings: List[List[int]], firstPerson: int) -> List[int]:
        d = defaultdict(list)
        for x,y,time in meetings:
            d[x].append((time,y))
            d[y].append((time,x))
        d[0].append((0,firstPerson))

        ans = set()
        h = [(0,0)]
        while h:
            t, x = heappop(h)
            if x in ans: continue
            ans.add(x)
            for knowTime, y in d[x]:
                if y not in ans and knowTime>=t:    
                    heappush(h, (knowTime, y))

        return ans  

其中的if ... knowTime>=t :還可以優化。

如果在建圖的時候先對時間做排序，則這裡可以不需要for整個d[x]，而是可以用binary search找到x「在知道秘密之後所參與的最早的會議時間」。

會變成像這樣(注意最前面meetings要先對時間做排序)

Greedy: broadcasting

class Solution: def findAllPeople(self, n: int, meetings: List[List[int]], firstPerson: int) -> List[int]: meetings.sort(key=lambda x: x[2])

    ...

    while h:
        
        ...

        for knowTime, y in d[x][bisect.bisect_left(d[x], t, key = lambda x: x[0]):]:
            if y not in ans:    
                heappush(h, (knowTime, y))

複雜度分析

在worst case中，heap的最大長度會有 n + m (n,m分別是總人數與meeting數) heap push與pop操作均消耗log(n+m)

因此總時間複雜度為 T = O( (n+m) log (n+m) )

空間複雜度可視為建立圖與heap的 S = O(n+m)

結語

因為感冒所以這篇寫了好幾天，該死的病毒。

Leetcode上對於這題也有非常詳細的官方講解，在這裡標註一下與本文解法的對應關係：

Leetcode Approach 3 = 本文方案三

Leetcode Approach 4 = 本文方案一

Leetcode Approach 5 = 本文方案二

基於root所實作的Union Find在圖論題是很強大的工具，但是實作的時候一定要考慮rank來優化(維護)樹的高度越小，不能發懶，因為一定會有測資故意設計出來搞你= =

順帶一題一個Contest小技巧是，像這種碼起來很麻煩的演算法練習幾次熟悉之後就可以寫成一個Class然後直接貼進來用，可以節省Contest的時間。

題外話，筆者本題倒是比較喜歡「不用圖論」的方案三解法，比較接近正常人的人腦「照著題目的秘密傳播規則去想」會得出的解法。

感謝你的閱讀，如果有不同的想法或心得，歡迎留言一同討論！