題目分析

題目

請問這是程式競賽還是閱讀能力競賽？

You are given a 2D array points of size n x 2 representing integer coordinates of some points on a 2D-plane, where points[i] = [xi, yi].

We define the right direction as positive x-axis (increasing x-coordinate) and the left direction as negative x-axis (decreasing x-coordinate). Similarly, we define the up direction as positive y-axis (increasing y-coordinate) and the down direction as negative y-axis (decreasing y-coordinate)

You have to place n people, including Chisato and Takina, at these points such that there is exactly one person at every point. Chisato wants to be alone with Takina, so Chisato will build a rectangular fence with Chisato’s position as the upper left corner and Takina’s position as the lower right corner of the fence (Note that the fence might not enclose any area, i.e. it can be a line). If any person other than Chisato and Takina is either inside the fence or on the fence, Chisato will be sad.

Return the number of pairs of points where you can place Chisato and Takina, such that Chisato does not become sad on building the fence.

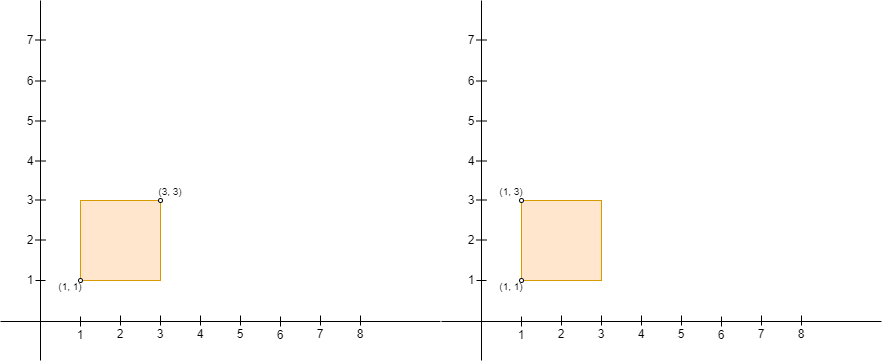
Note that Chisato can only build a fence with Chisato’s position as the upper left corner, and Takina’s position as the lower right corner. For example, Chisato cannot build either of the fences in the picture below with four corners (1, 1), (1, 3), (3, 1), and (3, 3), because:

With Chisato at (3, 3) and Takina at (1, 1), Chisato’s position is not the upper left corner and Takina’s position is not the lower right corner of the fence. With Chisato at (1, 3) and Takina at (1, 1), Takina’s position is not the lower right corner of the fence.

百合空間

Example 1:

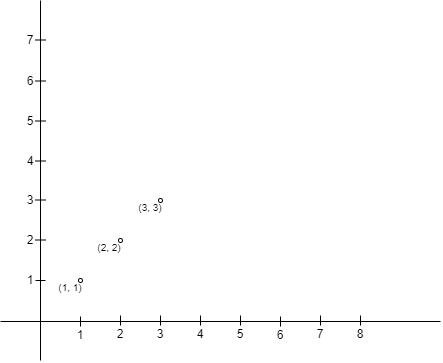
alt text

Input: points = [[1,1],[2,2],[3,3]]
Output: 0
Explanation: There is no way to place Chisato and Takina such that Chisato can build a fence with Chisato's position as the upper left corner and Takina's position as the lower right corner. Hence we return 0.

Example 2:

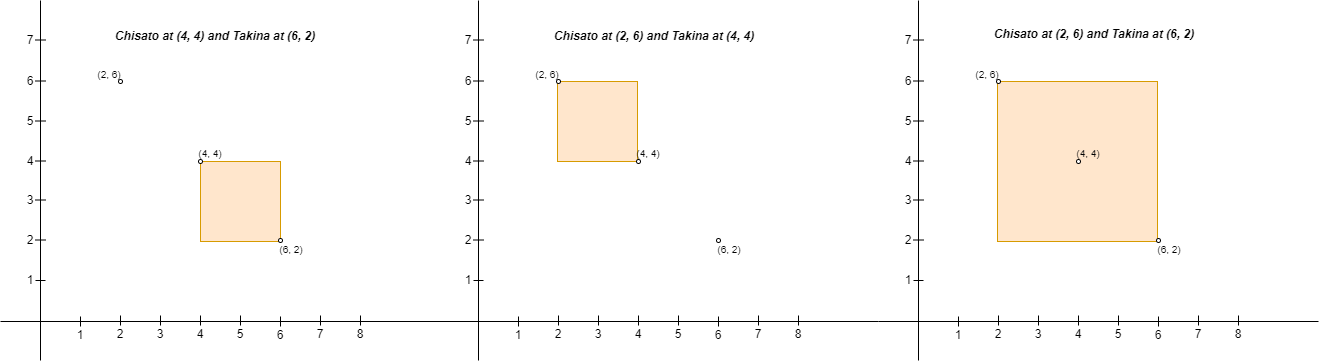
alt text

Input: points = [[6,2],[4,4],[2,6]]
Output: 2
Explanation: There are two ways to place Chisato and Takina such that Chisato will not be sad:
- Place Chisato at (4, 4) and Takina at (6, 2).
- Place Chisato at (2, 6) and Takina at (4, 4).
You cannot place Chisato at (2, 6) and Takina at (6, 2) because the person at (4, 4) will be inside the fence.

Example 3:

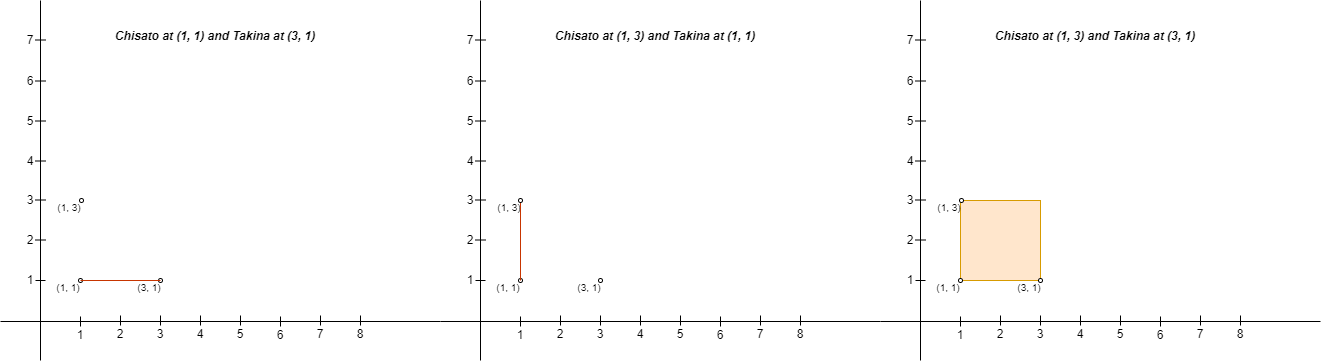
alt text

Input: points = [[3,1],[1,3],[1,1]]
Output: 2
Explanation: There are two ways to place Chisato and Takina such that Chisato will not be sad:
- Place Chisato at (1, 1) and Takina at (3, 1).
- Place Chisato at (1, 3) and Takina at (1, 1).
You cannot place Chisato at (1, 3) and Takina at (3, 1) because the person at (1, 1) will be on the fence.
Note that it does not matter if the fence encloses any area, the first and second fences in the image are valid.

Constraints:

2 <= n <= 1000
points[i].length == 2
-10^9 <= points[i][0], points[i][1] <= 10^9
All points[i] are distinct.

備註：

因為只有 3025. 偷發千瀧廚所以我這邊放的是3025的題目。

因為題目已經很長了所以就不放中文了，如果想看中文題目可以自行 ChatGPT 或者去中文哩扣看

分析

簡單整理一下題目的要求吧！

題目指定左下為座標原點的笛卡耳坐標系，亦即右方為+x，上方為+y。
題目給予points，裡面是每個不重複的點的座標，每個點都要配置一個人。
假設有兩個點 p1、p2分別給千束、瀧奈。千束只會站在左且上的點；瀧奈只會站在右且下的點。換言之，若兩個點呈右上－左下關係，就無法分配給她們。
也就是說，題目規範分給千瀧的兩個點可以成「左上右下」、垂直的「上下」，或者水平的「左右」關係。
當兩個點相對位置呈前述的關係時，可以將其分配給千瀧，並定義以p1為左上、p2為右下的矩形。
需要注意，由於兩個點允許呈垂直的「上下」，或者水平的「左右」關係，因此「矩形」可能為矩形，也可能為一條無面積的線。
若p1為左上、p2為右下所構成的矩形(包含矩形的邊界)中洽只有千瀧兩人(即無其他點)，則千束就會開心。我們姑且將其稱為「百合空間」吧！
求給定的所有points中，能讓千束開心的p1,p2數對的數量

懂了，也就是「介入百合之間的男人都該死」對吧。

LycoRis

回到題目的要求，首先可以確定的是：光是遍歷所有的p1,p2數對，就要花上O(n^2)的時間。

也就是我們需要一個能夠很快的判斷p1,p2數對能不能成為百合空間的策略。

咦？是不是有一個方法可以在O(1)內統計出某區間內的數量？

沒錯，就是我們在同一個Contest的第三題也拿出來用的 Prefix Sum！

2-D Prefix Sum 法

如果你不熟悉關於 1-D Prefix Sum 的基本觀念，建議先參考我在這篇文章關於Prefix Sum的介紹。以下的篇幅會以讀者充分理解 1-D Prefix Sum 的前提切入討論(不然篇幅真的會太長)

介紹 2-D Prefix Sum

我們都知道，對一個array，花費O(n) 來建立 Prefix Sum 之後，可以在O(1)時間內計算出任意給定 index= i,j 區間之內的 子陣列 總和。

把這個概念擴充至 2-D array，就稱為 2-D Prefix Sum。

注意：為配合題目的坐標系，本文所有範例中的矩陣都以左下角為原點

下圖為一個 2-D Prefix Sum 的示範：

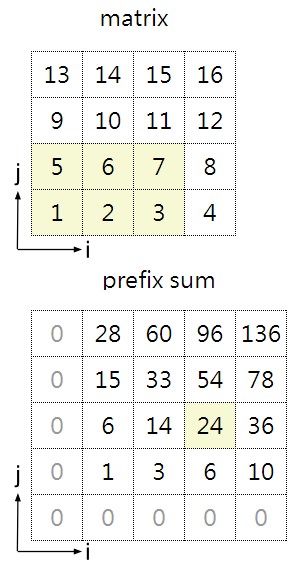
2DPSdefinition

可以發現，矩陣Prefix Sum的第(i+1, j+1)格的值，均恰為原矩陣matrix的(0~i,0~j)範圍矩陣的總和

例如圖中的ps(3,2)=24 恰等於m(0~2,0~1)的總和 1+2+3+5+6+7=24。

要如何建立一個 2-D Prefix Sum 呢？

建立 2-D Prefix Sum

如下圖：

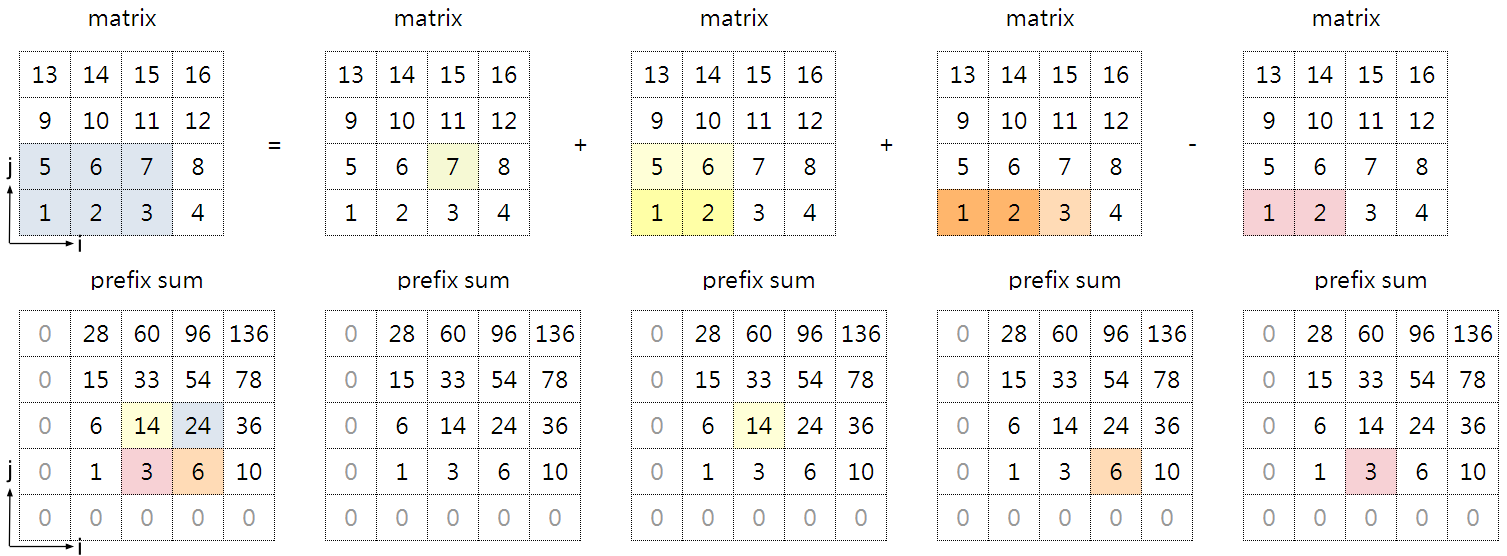
build 2D prefix sum

可以看出以下的公式：

所有 prefix(0,j) = prefix(i,0) = 0

prefix(i+1,j+1) = matrix(i,j) + prefix(i+1,j) + prefix(i,j+1) - prefix(i,j)

利用 2-D Prefix Sum 求矩陣和

如下圖：

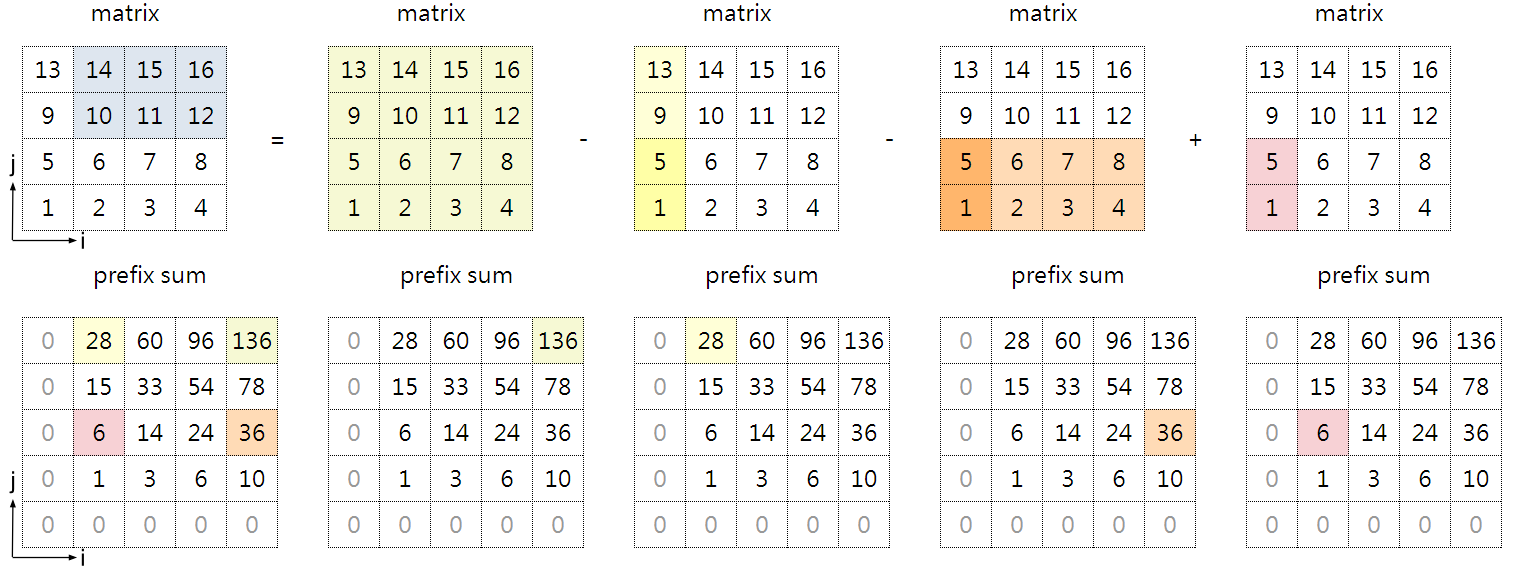
use 2D prefix sum to find sum of any submatrix

可知：

假設要求和的任意子矩陣，其座標範圍為 i = i1~i2 , j = j1~j2 (均包含)：

則其和 = prefix(i2+1,j2+1) - prefix(i1,j2+1) - prefix(i2+1,j1) + prefix(i1,j1)

解題思路

2-D Prefix Sum如何幫助我們解決這個問題？

方案一、2-D Prefix Sum + Coordinate Compression

利用矩陣和來統計子矩陣中的人數

一個很簡單的想法：我們就把座標空間中，「有人」的格子點全部放1，其他沒有人的點全部放0。

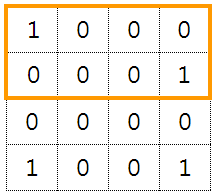
2D prefix count

這時候任意子矩陣的和，就代表其中的人數，恰好符合題目檢查百合空間中人數的需求！

不過，還有一個小問題：

本題的測資太大了！

-10^9 <= points[i][0], points[i][1] <= 10^9

從上圖可知，若我們要探討x,y座標介於0~3範圍內的點，就需要建一個4x4的矩陣。

而題目要求我們分析-10^-9 ~ 10^-9之間的座標！

雖然求值是O(1)，但建立 2-D Prefix Sum需要O(n^2)。因此若直接拿題目給的座標下去一定會爆炸。

所以這裡還需要一個小巧思！

座標壓縮

考慮以下兩種情況

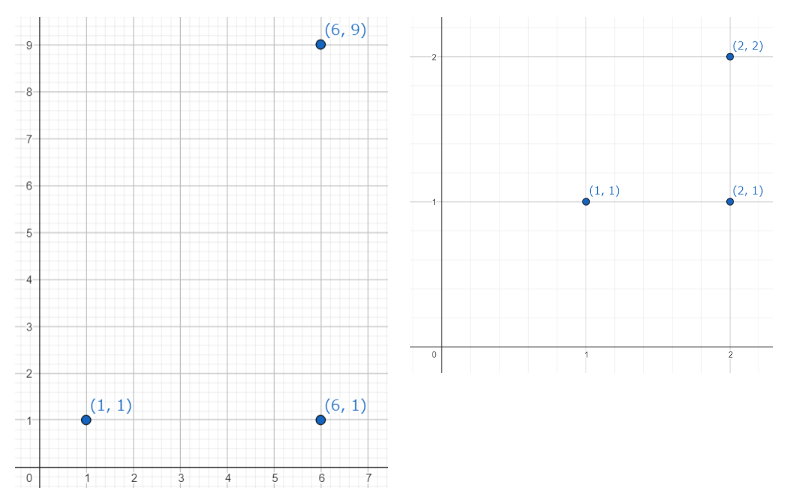
Coordinate Compression

對於百合空間的判定來說，是完全一樣的！

(都只有兩對可以)

換言之：

重要的是點與點之間的「相對位置」，而非絕對座標。

只有「有人在的x、y」座標需要建入prefix sum的陣列，其餘的通通可以忽略。

因此，可以使用「座標壓縮」( Coordinate Compression )的技巧：

將需要的x、y座標分別排序
將排序後的座標與其(在排序後的陣列中的)index一一對應，index即為該座標在壓縮之後的座標
以壓縮後的座標建立2D Prefix Sum

由於本題最多1000個點，所以最多會有1000個不同的x、y座標需要被考慮，我們只需要建立一個1000 x 1000的2D Prefix Sum，效能上是可以被接受的！

程式碼實作 (Python 3)

整個架構如下：

壓縮座標：取不重複的x、y分別排序
建立population matrix：有人的點設為1，其餘為0
套公式建立2D Prefix Sum
遍歷points，找出所有 p1-p2 pair
檢查並排除呈現「右上-左下」相對位置的 p1-p2 pair
套公式，利用2D Prefix Sum計算p1~p2矩陣的和

這裡需要注意：

前面的公式中，(i1, j1)與(i2, j2)分別為左下角和右上角

但這裡的(x1,y1)與(x2,y2)分別為左上角和右下角！

所以要畫個圖想一下要代什麼座標。
統計矩陣和=2的(百合空間)數量。

範例程式碼：

class Solution:
    def numberOfPairs(self, points: List[List[int]]) -> int:
        # coordinate compression
        # e.g. [[6,2],[4,4],[2,6]] --> [(2,0), (1,1), (0,2)]
        cc_x = {x:i for i,x in enumerate(sorted(set(p[0] for p in points)))}
        cc_y = {y:i for i,y in enumerate(sorted(set(p[1] for p in points)))}
        cc_p = list(map(lambda p:(cc_x[p[0]], cc_y[p[1]]), points))
        len_x, len_y, len_p = len(cc_x), len(cc_y), len(points)

        # build population matrix
        matrix = [[0]*len_y for _ in range(len_x)]
        for x,y in cc_p:
            matrix[x][y] = 1

        # build 2D prefix sum of matrix
        prefix = [[0]*(len_y+1) for _ in range(len_x+1)]
        for x in range(len_x):
            for y in range(len_y):
                prefix[x+1][y+1] = matrix[x][y] + prefix[x+1][y] + prefix[x][y+1] - prefix[x][y]
        
        ans = 0 # 紀錄百合空間的數量
        for i in range(len_p):  # 遍歷matrix，得到每一對p1,p2的組合
            for j in range(i):
                # 確保 p1 = 左/上 p2 = 右/下
                x1, y1 = cc_p[i] 
                x2, y2 = cc_p[j]
                if (y1<y2 and x1<x2) or(y1>y2 and x2>x2): continue # 右上 左下：跳過
                if (y1<y2) or (x1>x2): # p1下 或 p1右：交換
                    x1, x2 = x2, x1
                    y1, y2 = y2, y1
                
                # 計算 x1:x2  y2:y1 矩陣和 == 2 ，則為百合空間
                if prefix[x2+1][y1+1] - prefix[x2+1][y2] - prefix[x1][y1+1] + prefix[x1][y2] == 2:
                    ans += 1
        return ans

方案二、Sorting + Greedy (Boundary Check)

其實本題還有一個截然不同的策略：貪心算法！

這題的貪心思路搭配例題與圖片比較好理解：

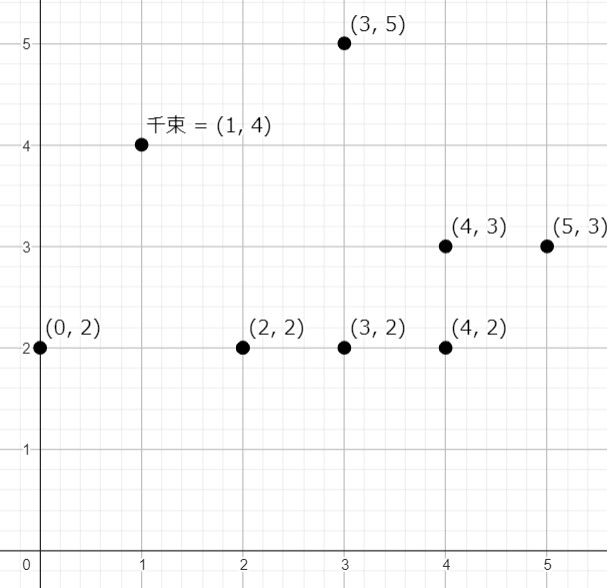
Greedy explaination question

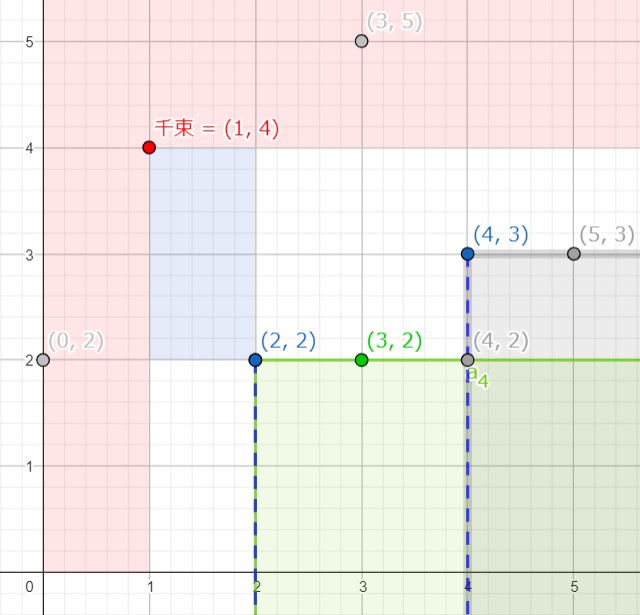
假設圖上的這些點，並且千束在(1,4)。那麼哪些點可以成為一個答案呢？

相信不用幾秒就能判斷出，瀧奈只能在(4,3)或者(2,2)

不過，大腦裡肯定沒有使用Prefix Sum來計算呀！

貪心算法的發想過程，往往在於把大腦的「直覺」給出的判斷，「拆解」成可執行的步驟，並且「驗證」其正確性。讓我們來試試看。

直覺(讓大腦猜答案)

我很確定就是(4,3)跟(2,2)，而且沒有其他的答案
因為他們離(1,4)比較近？
我由上往下逐點確認，所以或許跟排序有關？

拆解與驗證

或許在你的腦中是這樣依序剔除答案的？

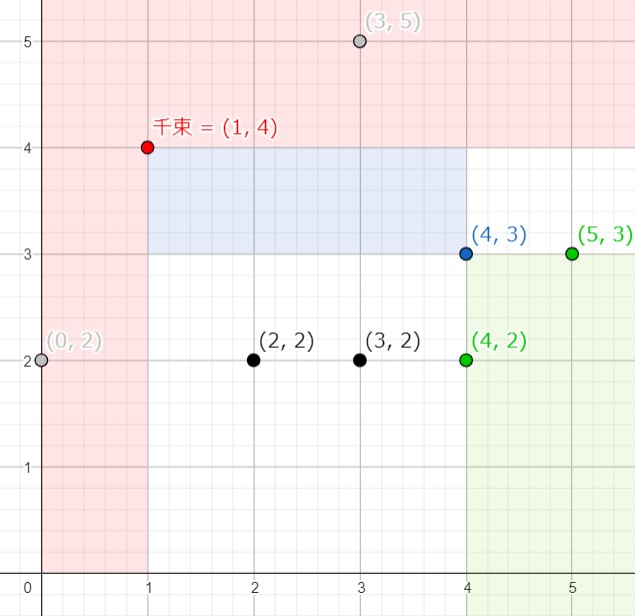
Greedy explaination 2

千束在(1,4)，且必須在瀧奈的右上/右/上。

因此，可以排除紅色區域 ( (3,5)和(0,2) )
在千束的右下方，由上至下、由左至右尋找，我們最先遇到(4,3)。因此，它是一個答案，而其右下方的綠色區域都不會是答案。

例如(5,3)，其位於(4,3)的右邊，因此從千束到(5,3)的矩形必定也將(4,3)包進去。

也就是說，我們先排除紅色區域，找到一組答案，並且排除綠色區域。

接下來，考慮(4,3)的下面一列之中未被排除的點：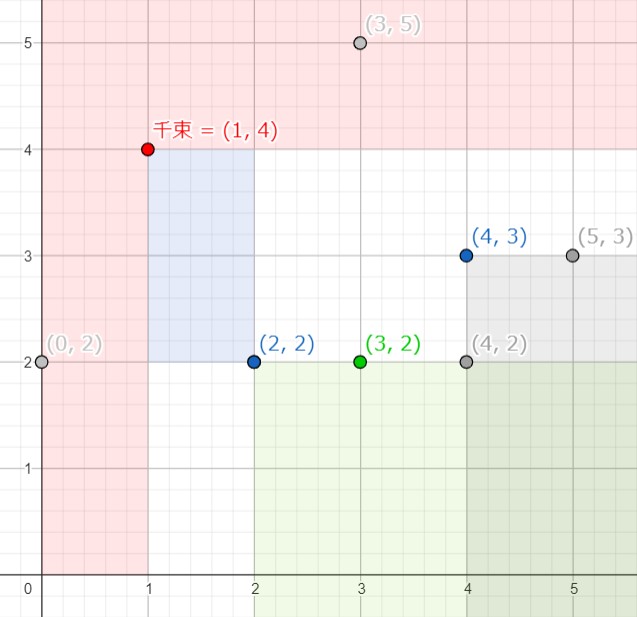
由左至右尋找，我們最先遇到(2,2)。因此，它是一個答案，而其右下方的綠色區域都不會是答案。

至此，我們建構出了一套完整的尋找/排除策略，只要一直執行下去，就可以找出/排除所有點的配對。

完整的貪心算法：

上述的策略可以概括如下：

將所有的點，先由上至下(y降序)排序；y軸相同的情況，由左至右排序(x升序)。
遍歷所有的點，並指定其為千束的位置。

假設我們目前指定了A點(上例中的(1,4))：
1. 遍歷所有排序在A點之後的點
  
  因為照y降序排序，所有位於A點上方的點(Y>Ya)並不在我們此時遍歷的範圍
  
  設定條件，排除所有位在A左邊的點，也就是所有X<Xa的點
  
  至此，排除所有的紅色區域。
2. 在尚沒有被排除的點中，排第一個的必可為瀧奈的位置。假設其為B點(上例中的(4,3))，答案計數+1
3. 記錄下B點的x座標Xb，並且接下來都排除位於B點正下方或右邊的點，也就是所有X>=Xb的點
  
  至此，排除了所有的綠色區域
4. 在尚沒有被排除的點中，排第一個的必可為瀧奈的位置。假設其為新的B點(上例中的(2,2))，答案計數+1
5. 更新 B點的座標，排除的條件不變(繼續排除X>=Xb的綠色區域)
6. 重複4~5，不斷找到新的答案、更新B點x座標，則剩餘的範圍就越來越窄。(下圖的藍色虛線，持續往左)
7. 等到Xb == Xa，就沒有瀧奈的位置了。結束這次迴圈，並且讓千束到下一個位置。

程式碼實作 (Python 3)

範例程式碼如下：

class Solution:
    def numberOfPairs(self, points: List[List[int]]) -> int:
        points = sorted(points, key=lambda x:(-x[1],x[0]))
        ans = 0
        for i,p in enumerate(points):
            x1= p[0]
            r = float('inf')
            for j in range(i+1, len(points)):
                x2= points[j][0]
                if x1<=x2 and x2<r: 
                    r = x2
                    ans += 1
        return ans

複雜度分析

方案一：複雜度O(n^2) 時間常數大

矩陣壓縮的部分使用到排序，故複雜度為O(n log n)

建立Matrix需要O(n^2)

建立Prefix Sum需要O(n^2)

遍歷所有的點對需要O(n^2) x 透過Prefix Sum計算矩陣和需要O(1)

整體複雜度 O(n^2)

方案二：複雜度O(n^2) 時間常數小

對點進行排序需要O(n log n)

遍歷所有的點設定為千束O(n) x 遍歷其後的點判定瀧奈O(n)

因此整體複雜度也是 O(n^2)

不過也很顯然的，因為不需要建矩陣，時間常數會小於prefix sum的算法。

貪心就是最棒的算法！貪心萬歲！！

heart escape

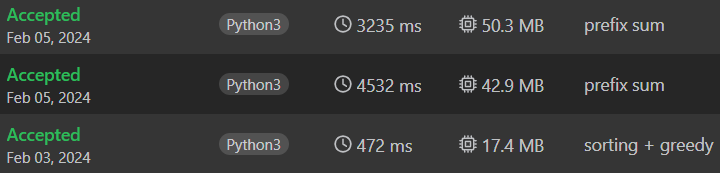
time complexity

註：Leetcode疑似有增添更多的測資，因此筆者後續再測，兩種算法的時間都比contest時增加很多倍。

結語

熟悉資料科學的話，對prefix sum應該不陌生。身為一個強大的陣列求和算法，用在這題看起來卻稍嫌不滿意，主要還是因為拿牛刀殺雞。

原本用來對整個陣列求任意矩陣和的算法被我們拿來加總0跟1，也真是委屈他了XD

感謝你的閱讀，如果有不同的想法或心得，歡迎留言一同討論！

Leetcode 3027. Find the Number of Ways to Place People II

目錄

題目分析

題目

分析

2-D Prefix Sum 法

介紹 2-D Prefix Sum

建立 2-D Prefix Sum

利用 2-D Prefix Sum 求矩陣和

解題思路

方案一、2-D Prefix Sum + Coordinate Compression

利用矩陣和來統計子矩陣中的人數

座標壓縮

程式碼實作 (Python 3)

方案二、Sorting + Greedy (Boundary Check)

直覺(讓大腦猜答案)

拆解與驗證

完整的貪心算法：

程式碼實作 (Python 3)

複雜度分析

方案一：複雜度O(n^2) 時間常數大

方案二：複雜度O(n^2) 時間常數小

結語

夏