今天 (2/8) 的 Daily 是 Medium 題: Leetcode 279. Perfect Squares
目錄
題目分析
雖然難度分類在Medium,不過這題除了使用標準的背包問題DP作答之外(並非最佳的效能),還有很巧妙的Greedy思維,本題更隱含了依賴數論定理的數學公式解法,能學到很多東西。
Leetcode也將這題列入動態規劃50題的題庫中。
題目
Given an integer n, return the least number of perfect square numbers that sum to n.
A perfect square is an integer that is the square of an integer; in other words, it is the product of some integer with itself. For example, 1, 4, 9, and 16 are perfect squares while 3 and 11 are not.
給你一個整數n,傳回和為n的完全平方數的最少數量。
完全平方數是一個整數,其值等於另一個整數的平方;換句話說,其值等於一個整數自乘的積。例如,1、4、9和16都是完全平方數,而3和11不是。
Example 1:
Input: n = 12
Output: 3
Explanation: 12 = 4 + 4 + 4.
Example 2:
Input: n = 13
Output: 2
Explanation: 13 = 4 + 9.
Constraints:
1 <= n <= 10^4
分析
題目要求:對於所有小於給定n的完全平方數,取出任意個並且使總和為n,求所有組合方式之中,最少的完全平方數個數。
並且透過Example 1.我們也了解到每個完全平方數可以重複取。
例如13 = 1+4+4+4 = 4+9 = 1+1+1+1+9 ...等
有複數種組合方法,要求裡面完全平方數個數最少的組合,也就是13=4+9,並返回其個數 2
第一感會發現到這是一個無限背包問題(Knapsack):
每個完全平方數可取0~無限個,並使其總和為n
解題思路
動態規劃 Dynamic Programming
對於這類的背包問題,有兩種動態規劃的思路:
動態規劃方案一、依序考慮所有平方數
例如我們要求 n = 10的答案
原問題可以描述成:
用[1,4,9]構成10,最少需要幾個平方數?
可以拆解成這樣的子問題:
用[1,4]構成10,最少需要幾個平方數?
再拆解成
用[1]構成10,最少需要幾個平方數
整個動態規劃的架構如下
-
首先,我們建立一個陣列dp,來記錄dp[i]「最少需要幾個平方數來組成這個i」
並先假設能使用的平方數只有 1,那對所有i,
dp[i] = i -
接著,考慮下一個平方數
4對於 i=4,因為本身即為平方數,將
dp[4] = 1對於
i=5,可以是5 = 1+1+1+1+1,因此原本記錄了dp[5] = 5但是,也可以是
5 = 1+4,也就是需要2個平方數這個2怎麼來的呢? 可以發現其為
dp[1] + 1因為要構成1,至少需要
dp[1](=1)個平方數,再加上一個4,構成5就需要2個兩種方案中,
2(1+4)<5(1+1+1+1+1),我們將dp[5]更新為較小的2接著考慮
i=6,原本dp[6] = 6,因為6=1+1+1+1+1+1但是也可以是
6 = 2 + 4透過
dp[2] = 2,我們知道要構成2至少需要2個平方數因此構成6至少需要
dp[2] + 1 = 3個平方數將
dp[6]從6更新為較小的3依此類推,將整個dp更新。
-
接著考慮下一個平方數9,依此類推遍歷所有小於或等於n的平方數。
-
最後,dp[n]即為構成n所需要的最少的平方數個數。
程式碼範例 (Python 3):
class Solution:
def numSquares(self, n: int) -> int:
dp = [i for i in range(n+1)]
for i in range(math.floor(math.sqrt(n))+1):
sq = i*i
for j in range(n+1):
if j-sq>=0:
dp[j] = min(dp[j-sq]+1, dp[j])
return dp[-1]
動態規劃方案二、依序考慮所有 n
原題目(假設要求n=10)可以描述成這樣:
用[1,4,9]構成10,最少需要幾個平方數?
可以拆解成這樣的子問題:
用[1,4,9]構成9,最少需要幾個平方數?
再拆解成
用[1,4,9]構成8,最少需要幾個平方數?
…依此類推。
則動態規劃的架構如下:
- 構成0,需要0個數(
dp[0]=0),即base case。 - 構成1,至少需要1個完全平方數(
dp[1] = 1) - 構成2,
2=1+1,需要2個完全平方數(dp[2] = dp[1]+1 = 2) - 構成3,
3=2+1,需要3個完全平方數(dp[3] = dp[2]+1 = 3) - 構成4,有兩種方法
- 從構成3的最佳解 + 1。即
dp[3] + 1 = 4 - 直接使用 4,或看成0 + 4,即
dp[0] + 1 = 1
- 從構成3的最佳解 + 1。即
- 構成5,有兩種方法,取較小者,
dp[5] = 2- 4+1,即
dp[4]+1 = 2 - 1+4,即
dp[1]+1 = 2
- 4+1,即
- … 依此類推至dp[10]
程式碼範例 (Python 3):
class Solution:
def numSquares(self, n: int) -> int:
dp = [0]
for i in range(1,n+1):
dp.append(
min( dp[i-root*root]+1
for root in range(1, math.floor(math.sqrt(i))+1)))
return dp[-1]
Greedy (Depth First Search + pruning)
動態規劃法雖為背包問題的標準解法之一,但不一定是最佳解法。
某些背包問題可以用貪心法得到更佳的效能,本題也是其中之一。
以 n = 15為例,來示範貪心的策略:能組成15的平方數有[1,4,9]
- 優先考慮最大的平方數:9。可以使用或不使用9
- 使用一個9,還需要6 (
15 - 9 = 6),能組成6的平方數有[1,4]-
使用一個4,還需要2(
6 - 4 = 2),能組成2的平方數有[1]- 使用兩個1。
13 = 9 + 4 + 1+1,共4個完全平方數。
- 目前最佳解:4個完全平方數。
- 使用兩個1。
-
不使用4,還需要6,能組成6的平方數有[1]
- 使用6個1。
13 = 9 + 1+1+1+1+1+1,共7個數。
- 目前最佳解:4個完全平方數。
- 使用6個1。
-
- 不使用9,還需要15。能組成15的平方數有[1,4]
- 最多可以使用3個4(
3x4 < 15),則剩下3(15-3x4 = 3) - 也可以使用0~2個4,但是因為剩下的平方數只有[1],故結果必定更差。
剪枝:目前最佳解:4個完全平方數。
因為在本分支內不可能得到比4更加的結果,結束本分支的討論。
- 最多可以使用3個4(
注意到這裡的計算順序,使用到遞迴,亦為一種DFS。
在原本的遞迴順序中,可能會考慮到所有的1~n,與所有的平方數(1~根號n)。因此複雜度為T = O(n x 根號 n)
複雜度跟前述的bottom-up動態規劃是相同的。(其實這正是top-down 動態規劃的順序)
但是在這個計算策略下,我們可以一併使用剪枝(pruning)策略:
- 在遞迴的時候我們不斷更新目前為止的最佳解
- 遞迴的順序從較大的平方數開始考慮
- 剪枝:如果在目前的遞迴分支上面,已經不可能比最佳解還要更好,就提前結束這個遞迴分支。
這個做法能大幅提升DFS的效能。
要如何設定剪枝的條件呢?
假定已計算的遞迴分支中最佳的答案為ans當我們計算到的遞迴分支上,已使用curCnt個完全平方數,還剩下curN需要被完全平方數組成,還能使用的完全平方數中最大者為maxSq
為了組合出curN至少需要curN // maxSq個完全平方數。
則當 curCnt + curN // maxSq >= ans 時可以直接結束遞迴。
程式碼範例 (Python 3):
class Solution:
def numSquares(self, n: int) -> int:
self.min = float('inf') # 紀錄最佳答案
self.dfs(n,math.floor(math.sqrt(n)),0) # 開始遞迴
return self.min # 回答最佳答案
def dfs(self, n, i, cnt): # n = 目標數
# i = 可使用的最大完全平方數的平方根
# cnt = 目前已使用的完全平方數個數
sq = i*i # sq = 可使用的最大完全平方數
if n%sq:
for k in reversed(range(n//sq +1)): # 可使用最多 n//sq 個 sq
if cnt+k >= self.min: #
return # 剪枝
self.dfs(n-k*sq, i-1, cnt+k) # 使用 k 個 sq 並繼續計算
else: # n 恰為 k 個 sq
self.min = min(cnt+n//sq, self.min) # 比較並更新答案
Math 數學公式解法
如果試著把不同n的答案印出來,會發現,答案好像都介於1~4之間。
實際上,根據數論定理Lagrange’s four-square theorem及幾個相關的定理:
- 任意正整數都可以被分割為四個非負整數的平方和
- 若某正整數可表示為
(4^a)(8*b+7),則無法分割成三個或以下正整數的和 (即答案=4)
因此,答案為1和4的可以透過簡單的判斷便得出。
答案為2和3的,只需遍歷i = 1~根號n並取其平方sq[i],並檢查n-sq[i]是否為完全平方數,若是則答案為2,否則答案為3。
範例程式碼:
class Solution:
def numSquares(self, n: int) -> int:
def isSquare(n):
return math.sqrt(n) == int(math.sqrt(n))
if isSquare(n): return 1
a = n
while a%4==0: a//=4
if a%8 == 7: return 4 # Lagrange's four-square theorem
for i in range(1,math.floor(math.sqrt(n))+1):
if isSquare(n-i*i): return 2
return 3
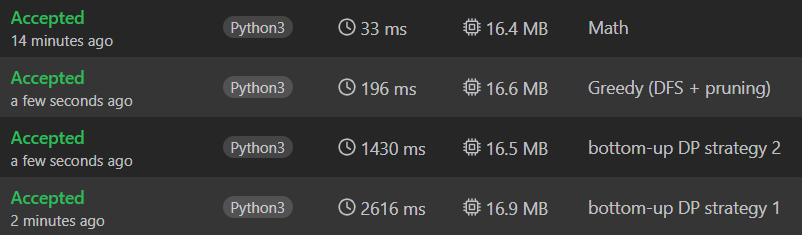
複雜度分析
動態規劃:時間複雜度為 T = O(n x 根號 n)
所提出的兩種做法只是內層loop與外層loop順序的差別,但是都分別對n和iloop。
因此時間複雜度為 O(n x i)
又因為 i平方(能夠使用的完全平方數) < n
因此時間複雜度為 O(n x 根號n)
Greedy(DFS + pruning):時間複雜度接近O(根號n),時間常數較大
因為答案必定為1~4,且剪枝的條件為「不可能比目前的最佳條件更小」
所以絕大多數的遞迴分支都會在O(1)的時間內被捨棄。
遞迴分支的總數不會超過i,也代表時間複雜度可以約略為O(根號n)
Math:時間複雜度接近O(根號n),時間常數小
答案為1的場合,複雜度為 O(1)
答案為2~3的場合,因為遍歷1~i檢查n是否為兩數的平方和,所以複雜度為 O(根號n)
答案為4的場合,複雜度為O(log n)
因此時間複雜度為O(根號n)
結語
正常人絕對想不到數學公式解,不過剪枝的優化很值得學習。對本題這種較極端的背包問題來說效果非常顯著。
感謝你的閱讀,如果有不同的想法或心得,歡迎留言一同討論!